Puissance moyenne consommée par un moteur électrique d'après ENAC

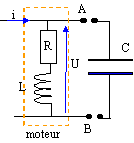
Un moteur M est alimenté par un courant alternatif sinusoïdal de fréquence f=50 Hz. Le moteur consomme une puissance moyenne Pmoy= 4,4 kW ; son facteur de puissance est cos j=0,6. U=220 V. Calculer l'intensité efficace I en ligne. - Calculer R et L. Le facteur de puissance du moteur est augmenté en connectant un condensateur de capacité C aux bornes du moteur. U=220 V - Que vaut C si cos j =0,9. - Quelle est la puissance moyenne absorbée par le moteur ? - Quelle est l'intensité du courant I1 en ligne ? corrigé Intensité efficace dans le moteur : Ieff= Pmoy / (U eff cosj) Ieff = 4400 / (220 * 0,6) = 33,33 A. La bobine inductive ne consomme pas de puissance ; la puissance est consommée dans le résistor : Pmoy = RI²eff soit R = Pmoy /I²eff =4400 / 33,33² = 3,96 W. 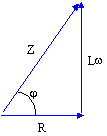la tension est en avance sur l'intensité : tan j = Lw/R soit L = Rtan j / w j =cos-10,6 = 53,13 rad ; w = 2pf = 314 rad/s. tanj = 1,333. ; L= 3,96 *1,333 / 314 =1,68 10-2 H = 16,8 mH. 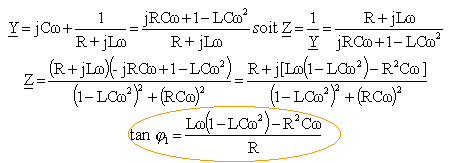Y admittance complexe, Z impédance complexe des deux branches en parallèle : cos j1 = 0,9 soit tan j1 = 0,484 0,484*3,96=0,0168*314(1-0,0168*3142C)-3,962*314C 1,916 = 5,27-8727C-4924C = 5,27-1,365 104C soit C= 2,46 10-4 F. autre méthode : Pactive = UIcosj Préactive = UIsinj Papparente = UI moteur seul 4400 W 5866 var 7333 VA + condensateur 0 -U2Cw= -2,17 107C 220 I1 total 4400 W -1,52 107C +5866 220 I1 cos j1 = 0,9 soit UI1 = 4400 / 0,9 = 4889 VA d'où I1 = 4889 / 220 = 22,2 A. sin j1 =0,436 ; -1,52 107C +5866 = 4889 *0,436 = 2131,6 C = 2,46 10-4 F. retour - menu