mouvements de particules chargées : champ électrostatique action d'un champ magnétique

action d'un champ électrostatique uniforme : accélération Une particule de charge q, de masse m, de vitesse initiale négligeable, est accélérée de électrodes A vers l'électrode B par une tension U=VA-VB. - Quel est le signe du produit qU ? Exprimer la vitesse finale de la particule. - Application numérique : compléter le tableau suivant relatif à un électron e = 1,6 10-19 C ; m = 9,1 10-31 kg. tension |U| 1 V 1 kV 1 MV vitesse atteinte m/s Fusion de noyaux légers : soit un cation de charge Q, ponctuel, fixe en O, origine d'un repère de coordonnées sphériques. - Exprimer le potentiel électrostatique crée par cette charge en un point de l'espace, puis l'énergie potentielle d'un ion de charge q situé à la distance r de Q ? - Exprimer l'énergie cinétique minimale K0 qu'il faut fournir à une charge positive (+ q), de masse m, initialement très éloigné de Q, fixe en O pour qu'elle puisse s'en approcher à la distance r. - Application numérique : un noyau de deutérium 21H est initialement très éloigné d'un noyau cible de tritium 31H ; r = 1 fm. 1/(4pe0) = 9 109 mF-1; Mproton = Mneutron = 1,67 10-27 kg . corrigé Le champ E est orienté dans le sens des potentiels décroissants. Si la tension U est positive, alors E est orienté de A vers B. La particule se dirige de A vers B sous l'action de la force qE : donc vecteurs champ et force sont colinéaires et de même sens : q>0 et qU>0. Théorème de l'énergie cinétique entre A et B : le poids étant très souvent négligeable devant la force électrique, on ne considère que le travail de celle-ci, soit : qU ½mv²-0 = qU soit v² = 2qU/m. 2|q|/m=2*1,6 10-19 / 9,1 10-31 = 3,52 1011. tension |U| 1 V 1 kV 1 MV vitesse atteinte m/s 5,93 105 1,87 107 5,93 108 L'électron ne peut pas dépasser la vitesse de la lumière. La mécanique classique ne peut pas être appliquée. fusion : Potentiel créé par un cation de charge Q à la distance OM= r : V= Q/(4pe0) r-1. énergie potentielle électrique d'un ion de charge q, situé à la distance r : qV= qQ/(4pe0) r-1. Le cation n'est soumis qu' à une force électrostatique : Or la force électrostatique est conservative, l'énergie mécanique du cation est constante. à l'infini ( énergie potentielle nulle), l'énergie mécanique est sous forme cinétique Ec0. à la distance r, expression de l'énergie mécanique : ½mv²(r) + qQ/(4pe0) r-1. conservation de l'énergie mécanique : Ec0 = ½mv²(r) + qQ/(4pe0) r-1. Ec0 est minimale si la vitesse v(r) est nulle soit K0 = qQ/(4pe0) r-1. A.N : q = Q = e = 1,6 10-19 C; r = 10-15 m ; K0 =(1,6 10-19 )² *9 109 / 10-15 = 2,3 10-13 J 2,3 10-13 / 1,6 10-13 = 1,44 MeV.

action d'un champ magnétique Les vecteurs sont écrits en bleu et en gras I. Une particule chargée pénètre en O dans une région de l'espace où existe un champ magnétique uniforme et constant B dirigé suivant l'axe Oz. La vitesse v0 de la particule lorsqu'ele arrive en O est perpendiculaire à B. La valeur du champ de l'ordre du tesla et les caractéristiques des particules sont : - charge : quelque fois la charge élémentaire - vitesse : quelques centaines de m / s. - masse : inférieures ou égales à 10-25 kg. Montrer que le poids est négligeable devant la force magnétique. Montrer que le mouvement de la particule est uniforme. Montrer que la trajectoire est un cercle ; exprimer le rayon en fonction de v0, q, m et B. Application numérique : B= 10-3 T ; rayon du cercle r = 4cm ; calculer la vitesse des électrons. Sans aucun calcul supplémentaire, décrire la trajectoire si, en O : v = v0 + v1 uz.   II. On considère le dispositif ci-dessous. A1 et A2 sont les armatures métalliques planes perpendiculaires au plan de la figure. 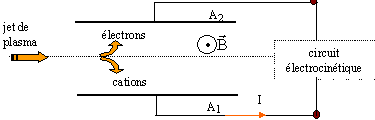Jet de plasma : mélange d'ions positifs et d'électrons. Sous l'action du champ magnétique les électrons et les cations sont déviés. Recueillis par l'armature A2, les électrons circulent dans le circuit électocinétique et rejoignent l'armature A1. On réalise ainsi un générateur qui fait circuler un courant I dont le sens conventionnel va de A1 vers A2 dans le circuit. Objectif : déterminer la force électromotrice de ce générateur. Les armatures étant initialement déchargées, le champ B est appliqué à partir de t=0 au jet de plasma. Que se passe au niveau des armatures A1 et A2 ; en déduire qu'on atteint un régime permanent dans lequel le jet de plasma traverse les plaques sans déviation. Montrer que ce régime permanent correspond à l'existence entre A1 et A2 d'un champ électrique E que l'on exprimera en fonction du champ B et de la vitesse v des particules du jet. A.N: v=500 m/s ; D=1 cm ( distance des armatures) ; B= 2 T ; en supposant le champ uniforme entre les armatures calculer la tension à vide VA1-VA2. corrigé poids de la particule : mg = 10-25 *10 = 10-24 N force magnétique |q|vB= 10-19*100*1=10-17 N soit 107 fois plus grande que le poids. le poids est négligeable devant la force magnétique. 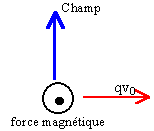La force magnétique est à chaque instant perpendiculaire à la vitesse v : donc cette force ne travaille pas et en conséquence ne modifie pas l'énergie cinétique de la particule. La norme de la vitesse est donc constante et le mouvement est uniforme. Le mouvement à lieu dans le plan défini par le champ B et le vecteur vitesse v, plan perpendiculaire à uz. 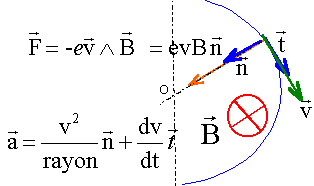La composante tangentielle de l'accélération est nulle ( mouvement uniforme). La composante normale est constante. mv²0/r = |q|v0B d'où r = mv0 /( |q|B). la trajectoire est un cercle de rayon r. A.N : v0= r|q|B /m= 0,04 * 1,6 10-19*10-3 / 9,1 10-31 = 7 106 m/s. cette valeur est inférieure à 10 fois la vitesse de la lumière dans le vide: on peut donc utiliser la mécanique classique. Si la vitesse initiale v posséde une composante suivant uz au mouvement circulaire uniforme dans le plan perpendiculaire à uz se supperpose un mouvement de translation suivant uz à la vitesse v1. La trajectoire est une hélice de rayon r = mv0 /( |q|B)et d'axe Oz. Sous l'action de la force magnétique les électrons sont déviés vers l'armature A2. Les cations sont moins déviés ( leur masse étant beaucoup plus grande que celle des électrons) : il est peu probable qu'ils atteignent l'armature A1. Entre les armatures , il en résulte un champ électrique E dirigé vers A2. Sous l'action de ce champ électrique les électrons sont soumis à une force supplémentaire F=-eE, dirigée vers A1, colinéaire à la force magnétique et de sens contraire. Le régime permanent est atteint lorsque ces deux forces sont opposées ( même norme) C'est le même principe que l'effet Hall. En régime permanent -eE -ev0^ B = 0 soit E = -v0^ B . La tension entre les armatures vaut : VA1-VA2 = ED = v B D= 500*2*0,01 = 10 V. retour - menu