étude de la troposphère ascension d'un ballon sonde

étude de la troposphère On note (Oz) l'axe vertical ascendant, z =0 au niveau du sol. g = -guz. On considère la troposhère ( altitude inférieure à 10 km) comme un gaz parfait. On note p(z) la pression, T(z) la température et v(z) le volume massique, p0 la pression au sol et T0 la température au sol. La troposhère est en équilibre ; elle obéit à la loi polytropique (1) : p-k(z) T(z) = p0-k T0 avec k = 0,15. Comment qualifie-t-on la transformation correspondant à k=0 ? - La troposphère est-elle homogène et isotrope - Ecrire l'équation d'état d'un gaz parfait à l'aide des paramètres p(z), v(z), R, Mair et T(z). loi notée (2) - Ecrire la loi fondamentale de la statique des fluides avec g,dp/dz et v(z). loi notée (3) Le gradient thermique est grad(T(z)) = -d uz. Exprimer d en fonction de k, Mair, g et R. Calculer d. - Ecrire la loi de variation de T(z) en fonction de d, T0 et z. Soit n moles de gaz parfait à l'altitude z. On note v(z) le volume à l'altitude z et v0 son volume au sol. Ecrire une relation entre v(z) et v0 en fonction de d, z, T0 et k. corrigé k=0 : p0(z) T(z) = p00 T0 --> T(z) = T0 transformation isotherme. Un milieu est homogène par rapport à une grandeur si celle-ci garde la même valeur en tous points du milieu. Dans un milieu est isotrope, toutes les directions sont équivalentes. La troposphère n'est pas homogène, pas isotrope du fait de la gravitation. Equation d'état de l'air considéré comme un gaz parfait : p(z) v(z) = RT(z) / Mair. loi (2) relation fondamentale de la statique des fluides : grad p= rg = g/ v. dans le cas d'un gaz compressible le volume massique dépend de la pression : v(z) grad p = g ; en projection sur l'axe (Oz) : v(z) dp/dz = -g loi (3). gradient thermique : la loi (1) donne : -k ln p(z) + ln T(z) = ln (constante) et en dérivant : soit dT/dz = k T(z) / p(z) dp/dz la loi (3) donne : dT/dz = -kgT(z) / [p(z) v(z)] la loi (2) donne : dT/dz = -kgMair/R gradient thermique : d = kgMair/R = 9,81*0,15*29 10-3 / 8,31 = 5,1 10-3 K m-1. ce gradient ne dépendpas de l'altitude z : la température diminue linéairement. T = T0-d z. volume d'une quantité de gaz constante : la loi (1) donne : p(z) = p0 [T(z)/T0]1/k = p0 [ 1- dz /T0]1/k--> p0 /p(z) = [ 1- dz /T0]-1/k la loi (2) donne : v(z) p(z) / T(z) = p0v0/ T0--> v(z) / v0 = p0 /p(z) *T(z) / T0 v(z) / v0 = [ 1- dz /T0]-1/k *T(z) / T0 or T(z) / T0 = 1-dz /T0 d'où : v(z) / v0 =[ 1- dz /T0]1-1/k .

ascension d'un ballon sonde on écrit les vecteurs en gras et en bleu. Masse totale du ballon avec instruments mB=1,2 kg. L'enveloppe est gonflée au sol avec n0 moles d'hydrogène. Son volume est v0. L'enveloppe se déchire et le ballon retombesi son volume dépasse la valeur vmax=10 v0. Quels sont les avantages et les inconvénients du dihydrogène. Ascension : une force de frottement Ffrot s'exerce sur le ballon. La somme des forces s'exerçant sur le ballon s'écrit : (F-mBg)uz + Ffrot. - Exprimer F en fonction de n0, g, MH2 et Mair. - Calculer la valeur minimale nmin de n0 permettant d'obtenir le décollage. - Calculer l'altitude maximale atteinte si T0 = 239 K. Le ballon s'étant déchiré ( trou pas trop gros) ne retombe pas immédiatement au sol. Il se vide lentement de son gaz. 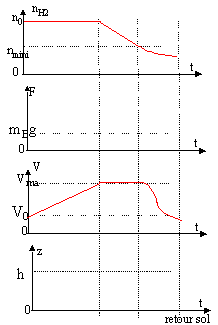La descente correspond au graphes suivants :- Compléter qualitativement les graphes F(t) et z(t). corrigé avantage de H2 : c'est le gaz ayant la plus petite masse molaire ; la force ascentionnelle sera très grande. inconvénient : gaz très inflammable. ascension à enveloppe fermée : F représente la pousée d'Archimède diminuée du poids du gaz H2 contenu dans le ballon. F= mair Vg - m H2 Vg ; or mair V = n0 Mair ; m H2 V=n0 MH2 ; F= g n0 ( Mair -MH2 ) Le ballon décolle si la somme vectorielle des forces appliquées sur le ballon est dirigée vers le haut. Dans le cas limite du décollage, la vitesse est nulle : donc la force de frottement fluide est nulle. F= mBg = g nmin ( Mair -MH2 ) soit nmin = mB/ ( Mair -MH2 ) nmin = 1,2 / [( 29-2)10-3 ]= 44,44 mol. l'altitude maximale est atteinte lorsque le volume maximal est atteint ; l'enveloppe se déchire. or v(z) / v0 =[ 1- dz /T0]1-1/k . vmax / v0 =10 = [ 1- dh /T0]1-1/k . 10k / (k-1) = 1- dh /T0 soit h = T0 /d (1-10k / (k-1) ) h = 239/ 5,1 10-3 ( 1-10-0,15 / 0,85) = 15,6 km. ce ballon permet d'explorer toute la troposphère dont l'épaisseur n'exède pas 10 km. cas d'une petite déchirure : la pression reste pratiquement la même à l'extérieur et à l'intérieur de l'enveloppe. La force F reste proportionnelle à la quantité de H2 enfermé. 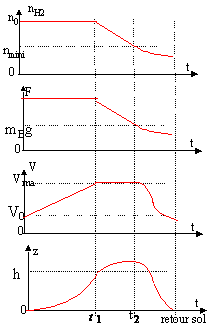F(t)= g nH2 (t) ( Mair -MH2 ) les deux graphes F(t) et nH2 (t) ont la même allure. durant l'ascension, le mouvement du ballon est rectiligne accéléré : z(t) est une courbe dont la concavité est dirigée vers le haut. Entre t1 et t2 le volume de l'enveloppe reste constant et nH2 diminue: le ballon continue à monter. à t > t2 , nH2 <nmin : en conséquence la somme vectorielle des forces appliquées au ballon est dirigée vers le bas: le ballon descend. La pression extérieure augmente, nH2 diminue donc le volume de l'enveloppe diminue. La vitesse d'arrivée au sol est différente de zéro. retour - menu