satellite Hipparcos télescope d'Hipparcos d'après Mines

satellite Hipparcos   Ce satellite devait être placé sur une orbite géostationnaire à 36000 km d'altitude. Un problème a laissé Hipparcos sur une orbite dont l'altitude varie entre h=500 km et H. Au cours d'une révolution, il passe dans la ceinture de Van Allen, ceinture comprise entre deux sphères de rayon r1 =8400 km et r2 = 28000 km, centrée sur la Terre. La terre est considérée comme une sphère de centre O, de rayon R= 6400 km et de masse M ; le satellite est assimilé à un point matériel (S, m). Le référentiel géocentrique d'étude est galiléen. La période de rotation de la terre dans ce référentiel appelé jour sidéral vaut T=86164 s. On note G la constante de gravitation. Moment cinétique : - Exprimer le moment cinétique L en O du satellite. Ce moment cinétique est-il constant ? - En coordonnées cylindriques (O, ur, uq, uz) avec uz tel que L=Luz, montrer que ce mouvement est plan, et exprimer r²q' en fonction de L et m. Comment nomme-t-on cette grandeur ? Vecteur excentricité : - Montrer que e= uq -L/(GmM)V est une constante du mouvement ( V étant le vecteur vitesse du satellite) - On choisit l'origine de l'angle polaire pour avoir q=(e, uq ). Montrer que l'équation de la trajectoire peut se mettre sous la forme r(q) = p/(1-e cosq) où e est la norme de e. En déduire la trajectoire du satellite. Trajectoire : - Exprimer et calculer e et p en fonction de h, H et R. - Exprimer et calculer le demi grand axe a de la trajectoire. Période d'Hipparcos : - Enoncer la 3ème loi de Kepler. - Exprimer la période Th de révolution d'Hipparcos en fonction de T, R, H et h. Calculer Th en heure. Ceinture de Van Allen : - Calculer les angles q1 et q2 d'entrée et de sortie dans la ceinture de Van Allen du satellite. - Schématiser la trajectoire du satellite et l'aire balayée lors du passage dans la ceinture de Van Allen. - Déterminer le rapport r =t0/Th en fonction de A et Ae ( aire de l'ellipse ) où t0 est la durée totale d'inactivité d'Hipparcos sur une période. On donne l'aire de l'ellipse : Ae= p p²/ ( 1-e²)3/2. Prendre A=200 106 km².   corrigé Le satellite est soumis à la force de gravitation de la terre (1). 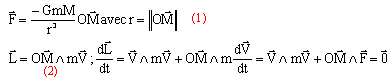Exprimer le moment cinétique en O du satellite (2) ; puis dériver cette expression (2) par rapport au temps : Cette dernière expression est nulle car le produit vectoriel de deux vecteurs colinéaires est nulle : en conséquence la dérivée du moment cinétique par rapport au temps est nulle et le moment cinétique est constant. Le vecteur moment cinétique est, à chaque instant, orthogonal au vecteur position et au vecteur vitesse ; de plus L est constant et dirigé suivant Oz. Le mouvement s'effectue dans un plan perpendiculaire à uz. Expression du moment cinétique L en coordonnées cylindriques : L = m r ur^ (r' ur+ rq' uq) = m r2q' uz. C= r2 q' = L/m est la constante des aires . vecteur excentricité : Dériver l'expression de e par rapport au temps puis faire le produit scalaire e.uq. 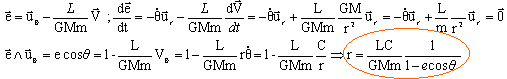La trajectoire est une ellipse de foyer O, d'exentricité e et de paramètre p= L2 (GMm2)-1. r = p (1-e cosq)-1. trajectoire : à l'apogée :  R+H= p / (1-e) ; au périgée : R+h= p / (1+e) d'où e= (H-h) (2R+H+h)-1 e = (3,6 107-5 105) (1,28 107 + 3,6 107+ 5 105)-1=3,55107*(4,93 107)-1=3,55/4,93=0,72. p = 2(R+H)(R+h) (2R+H+h)-1 ; p= 2(6,4 106+3,6 107)(6,4 106+5 105)(1,28 107 + 3,6 107+ 5 105)-1 p=2*4,24 107 *6,9 106*(4,93 107)-1=1,187 107 m. le grand axe de l'ellipse est la distance apogée-périgée; le demi-grand axe vaut a = R+½(H+h) période : pour les planètes solaires, le rapport a3/T2 est constant : a3/T2 = GMsoleil / (4p2) 3ème loi de Kepler Appliquer cette loi au satellite Hipparcos : a3/Th2 = (R+H)3/T2 = GMsoleil / (4p2)d'où Th2 =T2 a3(R+H)-3 Th = T(R+½(H+h))3/2(R+H)-3/2 Th = 86164(6,4 106 + 0,5*3,65 107)3/2(4,24 107)-3/2 Th = 86164*1,224 1011*3,62 10-12 = 38178 s = 10 h 36 min. ceinture de Van Allen : r = p (1-e cosq)-1. entrée dans la ceinture : r1 =2,8 107 m : 1-e cosq1 = p/r1 ; cosq1= e-1(1-p/r1) avec e = 0,72 et p = 1,187 107 m. cosq1=0,72-1(1-1,187/2,8) = 0,8 et q1 = 37°. sortie de la ceinture : r2 =8,4 106 m : cosq2= e-1(1-p/r2) cosq2=0,72-1(1-1,187/0,84) = -0,573 et q1 = 125°. 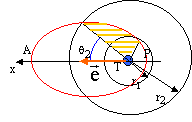Durant une période, Hipparcos traverse deux fois la ceinture de Van Allen; d'après la seconde loi de kepler la vitesse aréolaire est constante et la durée t0 d'inactivité est : t0 = 2ThA/ Ae doù r =2A/ Ae r =2A(1-e²)3/2/ (p p²)= 2*2 108 (1-0,72²)3/2 / (3,14*1,187² 108) = 4* 0,334/ 4 ,424 = 0,31 Hipparcos reste une bonne source de renseignements car r est faible

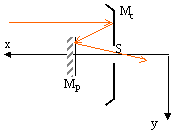
télescope d'Hipparcos Ce télescope est modélisé par un miroir concave Mc de rayon R=2800 mm et un miroir plan Mp de renvoi. Après deux réflexions la lumière passe par un orifice dans le miroir concave et atteint le détecteur, grille de cellules CCD. La grille comporte N= 2688 fentes équidistantes de l = 8,2 mm. Une étoile E est visée dans la direction Sx. Calculer l'abscisse x de l'image E1 de l'étoile E donnée par le miroir Mc. - "a " distance séparant le miroir plan à S. A quelle condition l'image finale E2 se forme-t-elle sur le détecteur placé à l'arrière du miroir concave ? - Calculer la valeur angulaire ac ( en degré) du champ observé. En réalité Hipparcos réalise une mesure de position relative des étoiles. Le télescope vise deux directions symétriques par rapport à Sx présentant un angle b=58°. Ainsi on obtient avec une grande précision l'angle entre deux étoiles. C'est un système de deux miroirs plans M1 et M2 qui permet d'obtenir les images des deux étoiles sur le détecteur. Le télescope tourne autour d'un axe de direction Sz avec une période T= 128 min. On supposera que la direction Sz est fixe bien que cet axe se déplace lentement afin de viser toute la sphère céleste. - Déterminer l'angle j 0 des miroirs M1 et M2 avec l'axe Sx du télescope. - Déterminer le déplacement angulaire q 1 d'un rayon lumineux réfléchi par le miroir M1 lorsque le satellite tourne d'un angle q. Préciser le sens de déplacement des rayons réfléchis par M1 et M2. - Quelle est la norme V de la vitesse de déplacement des images sur le détecteur.   corrigé L'objet visé est à l'infini sur l'axe du miroir, son image E1 est au foyer image du miroir concave, soit à l'abscisse x1 : x1 = SE1 = ½R = 1400 mm. L'image E2 est le symétrique de E1 par rapport au miroir plan. E2 doit être sur le détecteur : ce qui est écrit en bleu et en gras est une grandeur algébrique. SE2 = 2E1Mp-a = 2(a-x1)-a = a-2x1 <0 soit a<0,25 R. 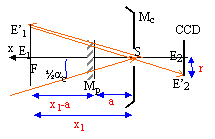La dimension du détecteur limite le champ observé: E'2 est l'image extrème se trouvant sur la dernière fente. Elle est le conjugué de E'1 par le miroir plan ( E'1 étant l'image d'une étoile à l'infini dans la direction ½ac) Les rayons incidents frappant le miroir concave en S sont réfléchi sous le même angle : ½ac = E'1E1/x1 = 2r / R = (N-1)l/R soit ac = 2(N-1)l/R = 2*(2688-1)*8,2 10-6/2,8=1,57 10-2 rad. 1,5710-2*180/3,14 = 0,9°. 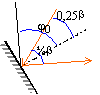angle de visée : j 0= ½p-0,25b= 90-58*0,25 = 75,5°. Quand le satellite tourne d'un angle q, les rayons réfléchis par M1 et M2 tournent de 2q dans le même sens. La vitesse de déplacement des images sur le détecteur vaut : V= q ' x1 = 2p/T x1 V= 6,28/ ( 128*60) *1,4 = 1,15 10-3 m/s. retour - menu