Calculs d'intensités dans divers circuits

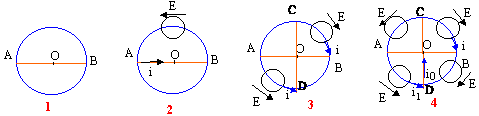
On réalise les circuits ci-dessus. Le conducteur AB a une résistance égale à 2r ; la section est du fil est constante, notée S. Exprimer la résistance équivalente R entre A et B (fig 1) en fonction de r. Exprimer i (fig 2) en fonction de E et r. Le générateur de tension est parfait. Exprimer les intensités i (traversant l'arc AD) et i2 ( traversant l'arc BD) fig 3, en fonction de E et r. Exprimer les intensités i0 et i1en fonction de E et r.(fig 4) corrigé La résistance du fil est proportionnelle à sa longueur ; lrésistance du demi-cercle : pr les deux demi-cercles et le diamètre AB constituent 3 résistances en dérivation entre A et B : les conductances (inverse des résistances s'ajoutent). 1/R= 1/(pr) + 1/(2r) + 1/(pr)= 2/(pr) + 1/(2r) = (4+p) / (2pr) R= 2pr /(4+p). 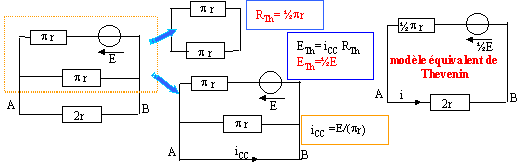On recherche le modèle équivalent de Thevenin du circuit encadré en pointillé : - en supprimant E, on trouve la résistance de Thevenin Rth = ½pr - en court-circuitant la branche AB on cherche l'intensité de court-circuit iCC. - on en déduit la f.e.m du générateur de Thevenin ETh = RTh iCC. i = Eth / ( Rth + 2r)=½E / (½pr +2r) = E / [(p+4)r]. 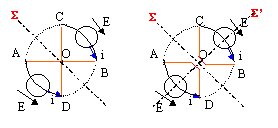Le montage est symétrique par rapport au plan S : - C et A sont donc au même potentiel et l'intensité dans la branche AC est nulle - B et D sont donc au même potentiel et l'intensité dans la branche BD est nulle. On peut supprimer les arcs AC et BD. Le montage est antisymétrique par rapport au plan S' : - l'intensité est la même dans les branches AO et OD. - l'intensité est la même dans les branches CO et OB. On peut déconnecter les brins au point O loi des mailles AOD : E= i ( ½pr + r+r) i = E / [r( ½p + 2)]. Le montage est antisymétrique par rapport au plan AB : - donc l'intensité est la même dans les branches CO et OD. Or la loi des noeuds en O impose la même intensité dans les branches AO et OB Le montage est symétrique par rapport au plan CD : - donc les intensités sont opposées dans les branches AO et OB En conséquence les intensités sont nulles dans les branches AO et OB et le conducteur AOB peut être supprimé. 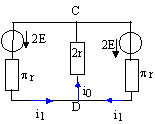i0 = 2i1. 2r i0 =2E - pri1soit 4r i1 =2E - pri1 ; i1 = 2E/[r(p+4)]. retour - menu