association lentille convergente et miroir points de Bravais Enac 01.

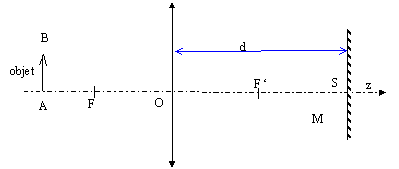
Une lentille convergente L a pour centre O, pour foyer F et pour foyer image F' ; sa distance focale image est f' >0. Un miroir plan M centré en S sur l'axe Oz de la lentille est disposé parallélement à celle-c à la distance d= 2f ' .   Un objet AB perpendiculaire à l'axe Oz est disposé de telle sorte que p=OA. Soit A1B1 son image après traversée de la lentilleL et réflexion sur M. Calculer OA1 en fonction de p. Ce qui est écrit en gras et en bleu est une grandeur algébrique Soit A2B2 l'image définitive de AB après traversée de la lentille L. Calculer OA2 en fonction de p. Trouver la condition à laquelle satisfait p lorsqu'il correspond à deux points de l'axe, dits points de Bravais, pour lesquels l'image A2B2 est dans le même plan que l'objet AB. En déduire les valeurs numériques p1 et p2 de p ( p1 < p2) qui satisfont à cette condition, sachant que f ' = 10 cm. Calculer les valeurs numériques g 1 et g 2 du grandissement transversal g correspondant respectivement aux abscisses p1 et p2 des points de Bravais. corrigé Soit A'B' l'image de AB à travers la lentille L. 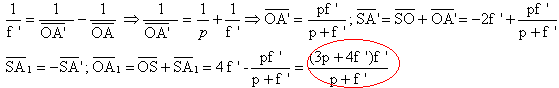La formule de conjugaison de Descartes donne : A1B1 est l'image de AB' dans le miroir ; A1B1 est symétrique de AB' par rapport au plan du miroir et en conséquent SA1 = -SA'. La seconde traversée de la lentille se fait dans le sens contraire de l'axe Oz : donc le foyer image est maintenant F. 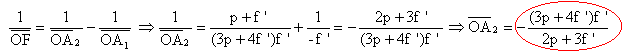La formule de Descartes s'écrit alors ( A1B1 objet et A2B2 image) : A est au point de Bravais si OA2 = p p(2p+3f ') = -(3p+4f ') f ' ; 2p² +3pf ' + 3pf ' +4f '² =0 p² + 3 f ' p + 2 f '² = 0 p doit être solution de l'équation du second degré ci-dessus p1 = -2 f ' et p2 = - f '. application numérique : p1 = -0,1 m et p2 = -0,2 m. 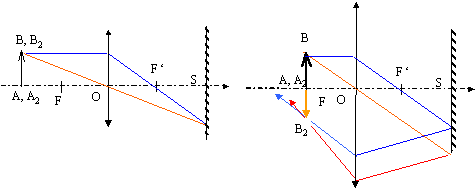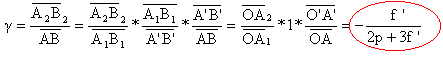grandissement transversal : dans les positions de Bravais, ce grandissement vaut g 1 = 1 et g 2 = -1.

retour - menu