Dynamique du point matériel ( référentiel galiléen) découvrir d'autres exercices " toute la physique et toute la chimie" par D Meier Chute verticale l'écureuil et le chasseur mobile et contre-poids le fil s'enroule sur le cylindre voile solaire

Chute verticale  les vecteurs sont écrits en gras et en bleu. Un point matériel de masse m, est abandoné sans vitesse initiale dans le champ de pesanteur terrestre. Exprimer la vitesse du point M dans les cas suivants : Chute libre ( sans frottement) Chute avec une force de frottement du type : F= -k v. Chute avec frottement du type : F= -k1 v v. corrigé La chute se fait suivant la verticale descendante. ( On choisit un axe Oz, vertical, orienté vers le bas, l'origine est situé à l'altitude h, moment du lâché). La force de frottement s'oppose au mouvement, elle est dirigée en sens contraire de l'axe Oz. Ecrire le principe fondamental de la dynamique sur l'axe Oz, le référentiel d'étude étant galiléen. mg + f = ma chute libre : mg = ma soit a=g. la vitesse est une primitive de l'accélération : v = gt+ Cte la vitesse initiale est nulle : la constante d'intégration est nulle. v= gt , indépendante de la masse m. chute avec frottement : mg + f = ma mg-kv=mz" = mv' ou v'+k/m v = g ou v'+ v/t =g avec t =m/k v'+ v/t =g (1) solution générale de l'équation v'+ v/t =0 : v= A exp(t/t ) solution particulière de (1) : vlimite = gt. solution générale de l'équation (1) : v = A exp(t/t ) +vlimite . à l'instant initial, la vitesse est nulle : 0= A+vlimite soit A= -vlimite . v = vlimite (1- exp(t/t ) ). mg-k1v²=mz" = mv' ou v'= g-k1/m v²= g(1-b²v²) avec b² = k1/(mg). v'= dv/dt= g(1-b²v²) . en séparant les variables vitesse et temps : dv / (1-b²v²) =gdt or 1 /(1-b²v²) = ½ /(1+bv) +½/(1-bv) primitive de dv /(1+bv) : 1/b ln(1+bv) ; primitive de dv /(1-bv) : -1/b ln(1-bv) ; d'où 1/b ln(1+bv) -1/b ln(1-bv) = gt +Cte la constante d'intégration est nulle car la vitesse initiale est nulle. ln[(1+bv) / (1-bv)]= b gt soit (1+bv) / (1-bv) = exp(b gt) ; 1+bv = (1-bv)exp(b gt) vb( 1+exp(b gt))=exp(b gt)-1 soit v = (exp(b gt)-1) / [b( 1+exp(b gt))]. la vitesse limite est : 1/b = (mg/k1)½.

l'écureuil et le chasseur Un écureuil, de masse m, se trouve sur une branche à l'altitude h par rapport au sol. Il aperçoit un chasseur qui pointe une arme sans sa direction. L'écureuil se laisse alors tomber vers le sol au moment où la pierre quitte la fronde. La pierre frappe-t-elle l'écureuil ?  ( le petit animal est assimilé à un point matériel) corrigé les vecteurs sont écrits en gras et en bleu. L'écureuil est en mouvement de chute libre verticale vers le bas, sans vitesse initiale. Le projectile a une trajectoire parabolique : la direction de la vitesse initiale du projectile pointe vers la position initiale de l'écureuil. référentiel galiléen : le sol ou la surface de la terre au pied de l'arbre. repère : (O,x,y) avec Oy dirigé vers le haut, origine au sol . Trajectoire de l'écureuil , initialement à l'abscisse x0 : yE= -½gt²+h ; xE=x0. Trajectoire du projectile, situé initialement à l'origine du repère : a(0 ; -g) ; v0(v0cosa ; v0sina) ; OM0 ( 0,0) vitesse, primitive de l'accélération : v(v0cosa ; -gt + v0sina) position, primitive de la vitesse : OM (xP=v0cosa t ; yP= -½gt² +v0sina t) trajectoire : t= xP / (v0cosa) ; repport dans yP : yP = -½g xP²/ (v0cosa)² + xP tana . A la date t1 de l'éventuelle rencontre : yP = yE et xP= x0 x0= v0cosa t1 et -½gt1² + h = -½gt1² +v0sina t1 soit h = v0sina t1 . v0 sina t1 / (v0cosa t1 ) = tan a = h / x0. l'écureuil saute et est touché par le projectile.

mobile et contre-poids L'objet de masse m se déplace sans frottement sur le plan incliné. La poulie a une masse faible et en conséquence la tension du fil est la même de chaque côté. Pour quelle masse m, le système est-il en équilibre ? Si m=3M, quel est le sens du mouvement ? Quelle est la tension du fil ? a=30° et m=1kg. corrigé Les deux solides sont assimilés à des points matériels. A l'équilibre l'accélération est nulle. référentiel terrestre galiléen. 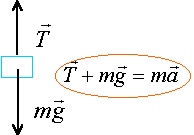le contre-poids est soumis à deux forces verticales : le poids mg, vers le bas et la tension du fil, vers le haut projection de la seconde loi de Newton sur un axe vertical, orienté vers le bas : mg-T=ma (1). 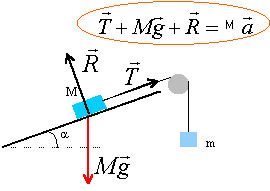ou a = g -T/m le mobile est soumis à trois forces : - le poids Mg, vertical vers le bas, la tension T du fil et l'action du plan R qui en l'absence de frottement est perpendiculaire au plan. projection de la seconde loi de Newton sur un axe parallèle au plan orienté vers le haut : -Mg sina +T=Ma (2) ; a = -gsina + T / M. or (1) donne T = mg-ma repport dans (2) : -Mgsina +mg-ma = Ma ; -Mgsina +mg = (M+m)a a = g( m-Msina ) / (M+m). à l'équilibre a=0 soit : m=Msina. si m=3M alors a = gM(3-sina ) /(4M)= 0,25 g(3-sina ) ; a est positive et M monte le plan tension du fil : T= m(g-a) = mg ( 1-0,25(3-sina))= 1*9,8(1-0,25 (3-sin30))= 3,675 N.

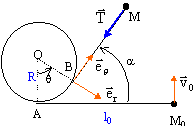
le fil s'enroule sur le cylindre Un cylindre d'axe vertical, de rayon R, est fixé sur un plan horizontal. On attache à sa base, au point A un fil de longueur initiale l0. L'autre extrémité est fixée à un solide de petite dimensions de masse M, astreint à glisser sans frottement sur le plan horizontal. ( voir figure : schéma en vue de dessus) A l'instant initial le solide est en M0 et on lui communique la vitesse v0. Le fil s'enroule sur le cylindre et reste tendu au cours du mouvement. Le fil est inextensible : quelle est la relation entre la longueur du fil non enroulé l(t) et l0, a(t), R ? Montrer que la norme de la vitesse reste constante au cours du mouvement. - En déduire l'angle a (t) en fonction de v0, l0, R et du temps. - Déterminer l'instant final où le fil est entierement enroulé autour du cylindre. corrigé les vecteurs sont écrits en gras et en bleu. a(t) = q(t),angles dont les côtés sont perpendiculaires. longueur de l'arc de cercle AB : Rq(t)=Ra(t) longueur du fil non enroulé : l(t) = l0-Ra(t). référentiel terrestre galiléen ; système : le point M est soumis à son poids P, l'action du support R (perpendiculaire au support et opposée au poids en absence de frottement), la tension T du fil. La seconde loi de newton s'écrit : P + R+T=ma= -Teq On utilise les coordonnées cylindriques (r,q,z) avec z=0 aucune force ne s'applique suivant er; la tension du fil modifie la direction du vecteur vitesse, tandis que la norme de la vitesse reste constante. vecteur vitesse : v = dOM/dt avec OM = R er+ l(t)eq v = R der/dt + dl(t) / dt eq + l(t)deq/dt Dérivée des vecteurs er et eq: les vecteurs er et eq ne dépendent que de l'angle q. Ces vecteurs se décomposent dans une base fixe ex et ey dans laquelle dex /dt et dey /dt sont nulles er = cos q ex + sin q ey et eq = -sin q ex + cos q ey. der /dt = -sin q q'ex + cos q q' ey et deq/dt = -cos q q' ex - sin q q' ey. der /dt =q'eq et deq/dt = -q'er par suite : v = R dq/dt eq + dl(t) / dt eq - l(t)dq/dt er or l(t) = l0-Ra(t) d'où en dérivant :dl(t) / dt = -Rda/dt = -Rdq/dt alors v = R dq/dt eq -Rdq/dt eq - l(t)dq/dt er soit v = - l(t)dq/dt er composante de la vitesse suivant er : vr = - l(t)dq/dt = constante = -v0. l(t)dq/dt = l(t)da/dt = v0 soit da/dt = v0 / l(t) angle a(t): dl(t)/dt = -Rda/dt soit dl(t)/dt = -R v0 / l(t) ou bien l(t) dl(t)/dt = -R v0. par intégration : ½l²(t) = -R v0 t + constante à t=0 , ½l0² = 0 + constante d'où : l²(t) = l0² -2R v0 t l(t) = [l0² -2R v0 t ]½ = l0-Ra(t) donne a(t) = R-1[l0-[l0² -2R v0 t ]½] l'angle a(t) augmente avec le temps. à l'instant final tf, la longueur du fil non enroulé est nulle. l(t) = [l0² -2R v0 tf ]½ =0 soit tf = l0² /(2R v0 ).

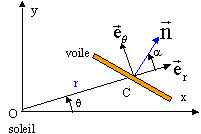
voile solaire On étudie le mouvement d'une voile solaire de masse m, de surface S et de centre de masse C. Le mouvement est supposé plan dans un référentiel galiléen lié au soleil. La voile est soumise à la force gravitationnelle FS due au soleil FS = -GmMS/r² er ( MS est la masse du soleil) et à la force F due au rayonnement solaire. F =k cos²a /r² n avec k=PS/(2pc); P puissance totale du rayonnement solaire ; c : vitesse de la lumière dans le vide ; l'angle a est constant. Montrer que l'accélération du centre de masse C est : a = Aer/r² +Beq/r². Exprimer A et B en fonction de G, m, k, i. - Ecrire les équations différentielles en r et q. Les vecteurs vitesse v et er font un angle F constant. - Montrer que d²r/dt²=r" = b/r² avec b un coefficient constant négatif. - Exprimer b en fonction de A, B et tan F. - Multiplier cette équation par r' et l'intégrer avec les conditions initiales suivantes : r(0)=r0 ; r'(0)=[-2b/r0]½. En déduire l'expression de r(t) sous la forme r(t) = r0 (1+ at)b. - Trouver la valeur numérique de b. - Exprimer a en fonction de b et r0. Commenter le signe de a. - Déterminer q (t) et l'équation de la trajectoire en prenant q (0)=0. corrigé accélération : référentiel galiléen lié au soleil ; système : le point C de masse m. Ecrire le principe fondamental de la dynamique : FS +F = ma Exprimer les forces dans la base polaire : ma = -GmMS/r² er +k cos²a /r² cos a er ++k cos²a /r² sin aeq . a = [-GMS/r² +k m-1 cos3a /r² ]er +k m-1 cos²a sin a /r² eq . en conséquence : A= -GMS +k m-1 cos3a ; B= k m-1 cos²a sin a . L'accélération s'écrit en coordonnées polaires : ar = r"-rq'² et aq = rq "+2r'q' les équations différentielles demandées sont : r"-rq'² =A/r² (1) et rq "+2r'q' = B/r² (2). à partir de la vitesse : Les vecteurs vitesse v et er font un angle F constant. v.er = vr = r'=v cos F et v.eq = vq = r q '= v sin F d'où l = tan F = vr /vq = r' / (r q ') (3). trouver b : éliminer la variable q dans les équations (1) et (2). (3) s'écrit : q ' = r' / (r l) ; dériver par rapport au temps ce quotient q" = 1 / l[r" / r -r'²/r²] (1) s'écrit : r"-r r'²/(r l) ² =A/r² soit r"- r'²/(r l ²) =A/r² (1') (2) s'écrit : r / l[r" / r -r'²/r²] +2r'² / (r l) = B/r² soit 1/l (r" +r'² / r) = B/r² (2'). (1') + l(2') donne : A/r² + l-1 B/r² = r"- r'²/(r l ²) + (r"l-2 + r'² l-2 / r) = r"(1+l-2 ) r" = 1/r² (A+ l-1 B) / (1+l-2 ) = b / r² soit b = (A+ l-1 B) / (1+l-2 ). intégration : multiplions chaque membre par r' : r' r" = b r' / r² avec r' r" = r' dr'/dt primitive de r' r" : ½ r' ²+Cte ; primitive de r' / r² : -1/r +cte. soit -b/r = ½ r' ² + Cte La constante se calcule à partir des conditions initiales : r(0)=r0 ; r'(0)=[-2b/r0]½. -b/r0= ½[-2b/r0] + Cte soit Cte =0. en conséquence : -b/r = ½ r' ² (4) la solution de (4) est de la forme : r(t) = r0 (1+ at)b. dériver par rapport au temps : r' = bar0(1+ at)b-1. repport dans (4) : -br0-1 (1+ at)-b=½ b²a²r0²(1+ at)2(b-1). cette expression doit être vérifiée quelque soit b : d'où : -b = 2(b-1) et : -br0-1 = ½ b²a²r0² soit b = 2/3 et a² = -2br0-3b-2. le signe de a est positif car la distance r=OC augmente avec le temps : la voile solaire s'éloigne du soleil. l = r' / (r q ') (3) élever au carré : l² = r' ²/ (r q ')² et -b/r = ½ r' ² (4) d'où l² =(-2b) r-3 q '-2 soit q ' = l-1(-2b)½ r-3/2 avec r(t) = r0 (1+ at)b. d'où q '=l-1 (-2b)½ [r0(1+ at)b]-3/2=l-1 (-2b)½ r0-3/2 (1+ at)-3b/2=dq/dt séparer les variables q et t : dq = l-1 (-2b)½ r0-3/2 (1+ at)-3b/2 dt remplacer b par sa valeur b =2/3 : dq = l-1 (-2b)½ r0-3/2 (1+ at)-1 dt primitive de (1+ at)-1 : a-1 log (1+at) + cte or a = (-2b)½r0-3/2b-1 d'où : q = l-1 (-2b)½ r0-3/2 a-1 log (1+at) + cte = l-1b log (1+at) + cte or à t=0 , q 0= 0 : la constante d'intégration est donc nulle  q =l-1b log (1+at) soit l-1 log (1+at)b avec r(t) = r0 (1+ at)b. q =l-1 log (r(t) / r0 ) soit r(t) = r0 e(q l). spirale logarithmique

autres exercices : glissade sur un igloo, looping, rotation d'un ressort retour - menu