éviter une catastrophe d'après Mines 01 du café chaud, mais non bouilli éviter de détériorer les composants électroniques mise sur orbite d'un satellite

Une casserole, sans couvercle, contenant un litre d'eau froide, est posée sur une plaque électrique chauffante. Initialement la plaque est froide et la température de l'eau est q=20°C. On relève la température de l'eau (homogénéisée par agitation) à différentes dates mesurées depuis la mise sous tension de la plaque. t (min) 0 1 2 3 4 5 6 7 8 q °C 20 21 25 31 39 48 58 68 78 Tracer la courbe représentant les variations de la température en fonction du temps. - On modélise la courbe à l'aide de deux segments de droite. L'un horizontal de t=0 à t=T et l'autre de coefficient directeur a. Déterminer graphiquement a et T. On défini le rendement du chauffage h=Q/W ; Q : énergie reçue par l'eau ; W : énergie électrique consommée. ceau = 4180 J Kg-1K-1. - La puissance électrique de la plaque est P=1500 W ; calculer le rendement h 1 lors du fonctionnement linéaire puis le rendement h 2 lors des 8 premières minutes de chauffe. Comment améliorer h 2 . On désire chauffer l'équivalent de huit petites tasses de café correspondant à 0,75 L. Le café, initialement à 20°C est placé dans une casserole sans couvercle sur la plaque de chauffe. Pour éviter l'ébullition et compte tenu du manque d'agitation pendant le chauffage, on se fixe comme limite de temps celle correspondant à une température de 70°C si la température était homogène. - Evaluer la durée maximale du chauffage en négligeant la capacité thermique du récipient. - Le résultat précédent est-il compatible avec la durée expérimentale ( avec agitation) : 6 min 15 ? 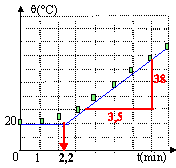corrigé T= 2,2 min ; coefficient directeur a = 38/3,5 = 10,8°C min-1= 10,8/60 °C s-1= 0,18°C s-1. rendement h 1 durant le régime linéaire : (masse d'eau 1 kg) énergie reçue par 1 kg d'eau : Q= m ceau Dq ; puissance reçue par l'eau : Q/Dt avecDt = durée (s) de la seconde phase Q/Dt = m ceau Dq /Dt = m ceau a puissance électrique : P. h 1 = a m ceau / P = 0,18 *1*4180 / 1500 = 0,50. rendement h 2 durant les huit premières minutes : h 2 = m ceau Dq / (PDt) h 2 = 1*4180*(70-20) / (1500*8*60)=0,26. Au début le rendement est faible car on doit chauffer la plaque électrique. On améliore h 2 en faisant un préchauffage de la plaque ( faire cuire autre chose auparavant) première phase incompressible : l'énergie électrique est utilisée au chauffage de la plaque puis la plaque chaude chaufffe l'eau et le récipient avec le rendement égal à h 1(0,75 kg d'eau est porté de 20 à 70°C). énergie reçue par l'eau : 0,75*4180*(70-20) = 156 750 J énergie électrique nécessaire : 156 750 / h 1 = 176 750 / 0,5 = 313 500 J énergie électrique consommée : PDt = 313 500 soit Dt =313 500 / 1500 = 209 s durée totale du chauffage : 2,2*60 + 209 = 341 s ou 5 min 41 s. valeur compatible avec la durée expérimentale de 6 min15s.

éviter de détériorer les composants électroniques On réalise un circuit RLC série : R0=25W , C=1mF; bobine r=15W et L=1H. Ce circuit est alimenté par la tension uE=Umax cos(wt) de valeur efficace U constante mais dont la fréquence peut être ajustée à toute valeur inférieure à 1kHz. On note uS la tension aux bornes du condensateur et H =uS / uE la fonction de transfert. On pose R=R0+r ; w 0²=1/(LC) ; Q= 1/(RCw 0) ; Gdb=20 log H avec H module de la fonction de transfert. Exprimer le module de la fonction de transfert en fonction de Q et x=w/w 0. Le résultat sera donné sous forme d'un quotient dont le numérateur sera égal à 1. - Calculer Q, le facteur de qualité. - Calculer la valeur x0 de x pour laquelle H est maximale. - Calculer cette valeur maximale Hmax. Calculer le module de la fonction de transfert pour x1= 1,0194 et x2=0,9794. Que représentent ces deux valeurs particulières ? Donner l'allure du graphe GdB=f(x). Sachant que la bobine et le conducteur ohmique ne peuvent supporter sans risque de destruction un courant d'intensité efficace 500 mA et que le condensateur est détruit lorsque la tension efficace à ses bornes atteint 200 V, à quelle valeur doit-on limiter U pour qu'aucun composant ne soit détériorer lorsque la fréquence varie de 0 à 1kHz..   corrigé les lettres soulignées sont les nombres complexes associés aux grandeurs physiques. impédance complexe du circuit RLC série : z = R+j(Lw-1/(Cw) d'où uE= z i ; impédance complexe du condensateur : 1/(jCw) d'où uS= i / (jCw); fonction de transfert complexe : H = uS/uE =1/(jCw(R+j(Lw-1/(Cw))= 1/D On note D = jCw(R+j(Lw-1/(Cw)=jRCw+ 1-LCw2. On multiplie numérateur et dénominateur par l'expression conjuguée : 1-LCw2-jRCw le numérateur est :1-LCw2-jRCw ; le dénominateur s'écrit : (1-LCw2)2+(RCw)2. norme de H : H=[(1-LCw2)2+(RCw)2]-½. Or LC= 1/w02 ; LCw2 = w2 / w02 = x2 ; Or RC= 1/(Qw0) ; RCw = Q-1w /w0=Q-1 x H=[(1-x2)2+Q-2 x2]-½. facteur de qualité : w0 = (LC)-½ = 103 rad/s. Q= 1/(40 10-6 103 )½ =25. H est maximale lorsque le dénominateur (1-x2)2+Q-2 x2 est minimal : (1-x2)2+1,6 10-3 x2 = 1+x4-2x2 +1,6 10-3 x2 = x4 -1,9984 x2 +1 dériver 4x3-3,9968x =0 la dérivée s'annule pour x=0 et x0= 0,9996. valeur correspondante du dénominateur : (1-0,99962)2+ 1,6 10-3 *0,99962)=1,6 10-7 +1,599 10-3 = 1,599 10-3 . Hmax = 1 / (1,599 10-3)½ = 25,01. H(x1) = [(1-1,0194²)²+(1,0194/25)²]-½ =17,68. H(x2) = [(1-0,9794²)²+(0,9794/25)²]-½ =17,69. H(x1) =H(x2) = Hmax / racine carrée (2) x1 et x2 sont les fréquences de coupure à -3dB. GdB = 20 logH=20*(-0,5)log[(1-x2)2+Q-2 x2]= -10log[(1-x2)2+Q-2 x2] recherche des asymptotes : si x <<1 , GdB tend vers zéro ; si x>>1 GdB tend vers -40 log x Q est important , donc résonance si x =x0=0,9996. 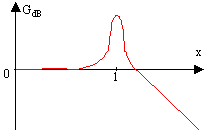L'intensité maximale est atteinte pour x=1 : l'impédance est minimale, égale à la résistance R. La fréquence vaut alors : w0 = 2p f soit f = 1000 /6,28 =159 Hz. La tension aux bornes du condensateur vaut alors QU = 25 U inférieur à 200V soit U <200/25 soit 8V. Imax = U/R avec Imax = 0,5 A soit R supérieure à 8/0,5 = 16 W.

mise sur orbite d'un satellite les vecteurs sont écrits en gras et en bleu. Dans le référentiel géocentrique supposé galiléen, un satellite de masse m = 400 kg, assimilé à un point matériel P, est en orbite autour de la terre de masse M= 6 1024 kg, supposée sphérique R= 6400 km. G= 6,67 10-11 m3s-2kg-1, constante de gravitation ; on pose k=GMm ; r : distance du centre de la terre au point P. On néglige toute force de freinage due à l'atmosphère terrestre. Déterminer l'expression de l'énergie potentielle Ep du satellite en fonction de k et r, l'énergie potentielle étant nulle à l'infini. Le satellite décrit une orbite circulaire à l'altitude h=aR avec a =0,05. Déterminer l'expression de la vitesse V0 en fonction de k, R et a. Calculer cette vitesse. Exprimer puis calculer l'énergie mécanique du satellite. La trajectoire n'est plus circulaire : - Démontrer que le moment cinétique s par rapport à O est constant et que la trajectoire est plane. - Le satellite est repéré par ces coordonnées polaire r et q. Exprimer dans ce système , le module du moment cinétique du satellite. Le satellite décrit l'ellipse d'équation polaire r= p / (1+e cosq) avec e excentricité ; e et p sont positifs. - Exprimer la valeur minimale de r , la valeur maximale de r et la valeur du demi grand axe a de l'ellipse en fonction de e et p. - Montrer que l'énergie mécanique du satellite est E= - k/(2a) rappels : constante des aire C=s/m ; formules de Binet : v² = c²(u²+u'²) avec u=1/r et u'= du/dq. p= mC²/k Le satellite situé au point P d'altitude h=aR, on lui communique une vitesse V perpendiculaire au rayon vecteur OP et de valeur V= bV0 avec V0 la vitesse lui permettant de décrire une orbite circulaire. Exprimer puis donner les valeurs de b afin que le satellite de s'écrase pas au sol, afin que le satellite n'échappe pas à l'attraction de la terre. corrigé Le satellite est soumis à la force de gravitation exercée par la terre, force attractive, dirigée suivant le rayon terrestre valeur de F : F= GMm/r² = k/ r2. L'énergie potentielle du satellite est alors Ep= - k/r ; Ep est nulle à l'infini. l'accélération du satellite est normale à la trajectoire ( accélération centripète) de valeur : aN=V02/r. La seconde loi de Newton s'écrit alors suivant un axe dirigé vers le centre de la terre : GMm/r2= maN=mV02/r soit V02 = GM/r avec r =R(1+a). V02 = 6,67 10-11 *6 1024 / ( 6,4 106*1,05)= 5,96 107 soit V0 = 7 710 m/s. L'énergie mécanique est la somme de l'énergie potentielle et de l'énergie cinétique. E= -k/r + ½mV02 avec V02 = GM/r sur une orbite circulaire E= -k/r + ½mGM / r =-k/r+½k/r = -½k/r E= -0,5*6,67 10-11*6 1024*400 / (6,4 106*1,05)= -1,2 1010 J. Le moment cinétique en O du satellite s'exprime : s0=OP^mv . dériver par rapport au temps : d s0/dt = dOP/dt ^mv +OP^mdv/dt = v^mv +OP^ma = v^mv +OP^F le produit vectoriel de deux vecteurs colinéaires est nul : d s0/dt =0 soit s0= constante. s0 est orthogonal au vecteur position OP et à la vitesse v. s0 vecteur constant, garde la même direction notée uz : la trajectoire est dans le plan xOy, perpendiculaire à uz. en coordonnées polaires le moment cinétique s'exprime : v = r' ur + r q'uq.  s0=OP^mv = r ur ^mr' ur + r ur ^m r q'uq=mr2q'uz. rmin = p/(1+e) ; rmax = p/(1-e) ; a= ½(rmin + rmax )=½p[1/(1+e) +1/(1-e)]=p/(1-e²). d'après les formules de Binet : u=(1+ecosq)/p ; u'= -e sin q /p V² = C²(u+u'²)=C²/p²[(1+ecosq)² + (e sin q )²]=C²/p²[1+e²+2ecosq] expression de l'énergie mécanique : E= -ku + ½ mV² = -k(1+ecosq)/p +½mC²/p²[1+e²+2ecosq] avec p=mC²/k E= -k(1+ecosq)/p+½k/p[1+e²+2ecosq]= ½k/p(e²-1) Or a = p/(1-e²) d'où E= -½k/a. Nouvelle expression de l'énergie mécanique du satellite : E= ½mV0²b² -k / r avec mV0² =GMm/r =k/r E= ½kb²/r - k/r = k/r(½b²-1) avec r=R(1+a) Le satellite échappe à l'attraction terrestre si son énergie mécanique est positive soit ½b²-1 >0 ou b²>2 Le satellite retombe sur terre si le grand axe de la nouvelle ellipse est trop petit : soit 2a<R+R(1+a) ; 2a<R(2+a) Or E= -½k/a soit E <-k/(R(2+a)) k/(R(1+a) )(½b²-1) <-k/(R(2+a)) ; (½b²-1)/(1+a) < -½/(2+a) (½b²-1)(2+a)< -(1+a) b²-2+½b²a-a <-1-a ; b²(1+½a)<1 soit b² < 1/ (1+½a). pour éviter la catastrophe il faut donc : b <1,414 et b >0,987. retour - menu