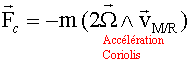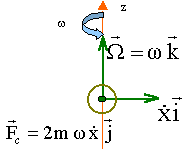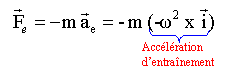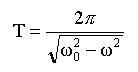|
travail, puissance, énergie
|
||
|
||
|
Un solide ponctuel M de masse m glisse sur une tige horizontale ; cette tige tourne à la vitesse w constante autour d'un axe vertical Oz fixe. Les frottements sont négligés. 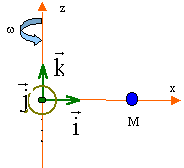 On choisit un référentiel R lié à la tige :
corrigé |
||
|
l'énergie cinétique de M s'écrit : Ec = ½ m x'². La tige est horizontale, alors l'énergie potentielle de pesanteur ne varie pas et on peut la choisir arbitrairement nulle ( en prenant l'origine des altitudes en O, origine du repère) le référentiel R n'est pas galiléen, il faut tenir compte des forces d'inertie : force d'inertie de
Coriolis :
La puissance de la force de Coriolis est nulle ( la force de Coriolis est perpendiculaire au vecteur vitesse). force d'inertie
d'entraînement : La puissance de cette force, colinéaire au vecteur vitesse n'est pas nulle : cette force dérive d'une énergie potentielle. travail de la force d'entraînement : l'énergie potentielle est l'opposé du travail : dEp = -mw²x dx Ep = -½mw²x² + Cte On choisit l'origine de cette énergie potentielle à l'abscisse x=0, dans ce cas la constante d'intégration est nulle. Energie mécanique de M : ½ m x'² -½mw²x² équation différentielle du mouvement de M : en absence de frottement l'énergie mécanique est constante ( la dérivée de l'énergie mécanique par rapport au temps est nulle) Pour obtenir l'équation différentielle du mouvement de M, dériver l'expression de l'énergie par rapport au temps. dérivée de x'² : 2 x" x' dérivée de x² : 2 x x' w est une constante. d'où : ½ m 2 x" x' - ½ mw² 2 x x' =0 diviser par m x' chaque terme : x" -w² x =0. La solution de cette équation différentielle est de la forme : x = A ch(wt) + B sh(wt) A et B sont des constantes qui dépendent des conditions initiales, non indiquées dans ce problème. Le mouvement ne peut pas être oscillatoire.
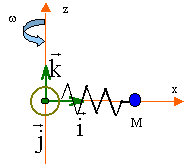
A l'énergie mécanique précédente il faut ajouter l'énergie potentielle élastique : Epé = ½ k(x-l0)² + Cte l'origine de cette énergie potentielle est prise à l'abscisse x = l0. Dans ce cas la constante est nulle. L'énergie mécanique s'écrit alors : ½ m x'² -½mw²x² + ½ k(x-l0)². celle ci est constante en l'absence de frottement équation différentielle du mouvement de M : la dérivée de l'énergie mécanique par rapport au temps est nulle Pour obtenir l'équation différentielle du mouvement de M, dériver l'expression de l'énergie par rapport au temps. d'où : ½ m 2 x" x' - ½ mw² 2 x x' + ½ k 2 (x-l0) x' = 0 diviser par m x' , supposée non nulle, chaque terme : x" - w² x + k /m (x-l0) =0. On pose w0² = k / m x" - w² x + w0² x = kl0/m x" + (w0² - w²) x = w² l0 (1) solution particulière de l'équation avec second membre : xe = w² l0 / (w0² - w²). On observe des oscillations autour de cette position d'équilibre si w0² > w² Dans ce cas, solution générale de l'équation sans second membre :
La solution générale de l'équation différentielle (1) est : xe + x1. A1 et A2 sont des constantes déterminées à partir des conditions initiales. La période des petites oscillations de M dans le référentiel lié à la tige est :
retour - menu |