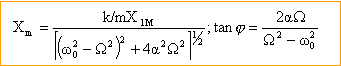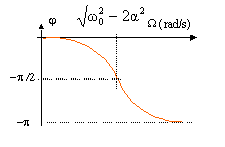|
|
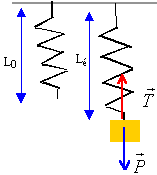
|||||||||
|
|||||||||
|
|||||||||
|
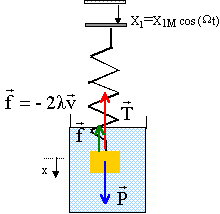
oscillations forcées : le support et la masse m sont en mouvement
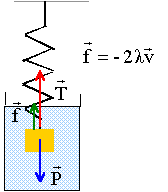
relation fondamentale de la dynamique projetée sur un axe verticale vers le bas : mx" = mg - 2a x'-k( Lé + x-X1-L0) or mg = k(Lé -L0) ; mx" = - 2l x' - kx + kX1 ; x" = - 2l /m x' - k/m x + k/mX1 ; x" +2a x'+ w0²x = k/mX1Mcos (Wt) (1) la solution de l'équation sans second membre est amortie exponentiellement : elle correspond à un régime transitoire. La solution particulière correspond au régime permanent. On se place au bout d'un temps suffisamment long pour que le régime permanent soit atteint : la solution de l'équation sans second memnbre est alors négligeable devant la solution particulière. l'excitateur force l'oscillateur à osciller à la fréquence de l'excitateur. X = Xm cos (W t+j) ou encore en notation complexe : X =Xm exp(jj) exp (jW t). dérivées : X' = Xm exp(jj) jW exp(jW t) ; X" = Xm exp(jj) (-W²) exp(jW t) ; repport dans (1) : -Xm exp(jj) W² exp(jW t) +2a Xm exp(jj) jW exp(jW t) + w0² Xm exp(jj) exp(jW t)= k/mX1Mexp(jW t) simplifcation par exp(jW t) : Xm exp(jj) (w0² -W² +2a jW ) = k/mX1M Xm (w0² -W² +2a jW ) = k/mX1Mexp(-jj)
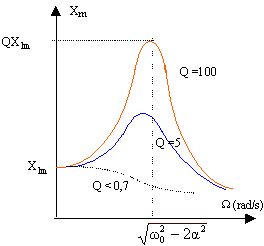
résonance d'amplitude ( d'élongation , de "tension") : pour quelles valeurs de la fréquence de l'excitateur, l'amplitude du résonateur est-elle maximum ? dériver Xm par rappot à W en posant u = [(w0² -W²)² +4a² W² ] -0,5 soit dXm / dW = k/mX1M (-0,5 u' u -1,5). u' = (w0² -W²)4W +8a² W = 4W ( w0² -W² +2a²) s'annule pour W=0 et W²= w0² -2a². ( w0² -2a² doit être positif) de plus Xm tend vers X1M quand W tend vers zéro et Xm tend vers 0 quand W tend vers l'infini. donc l'amplitude Xm passe par une valeur maximale quand W²= w0² -2a².
Q : facteur de qualité Q = w0 / (2a) valeur maximale d'autant plus
grande (résonance aigüe ) que l'amortissement
est faible.
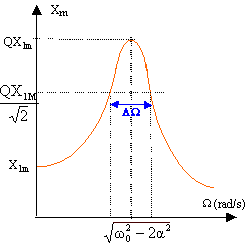
ensemble de pulsation telles que la valeur de l'amplitude Xm soit supérieure à 0,707 fois la valeur extremale.
tan j = 2aW /(W²-w0² ) la dérivée par rapport à W est négative : dj / dW = [2a(W²-w0² ) -4aW²]/(W²-w0² ) ² la fonction donnant le déphasage est décroissante de 0 à -p, en passant par -½p à la résonance. l'élongation est en retard sur l'excitateur.
retour - menu |