|
|
||
|
||
|
Un mobile P de petites dimensions, de masse m, est astreint à se déplacer sans frotement, dans le plan xOy à l'intérieur d' un guide parabolique d'équation y = x2/(2p). p constante positive. 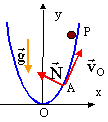 A la date t=0, le point P se trouve en A d'abscisse p, possédant la vitesse v0, tangente à l'arc de parabole. Le mobile est soumis à son poids et à l'action du support N, perpendiculaire à la vitesse en l'absence de frottement.
corrigé |
||
|
en A : Eméca = ½mv02 + mgy0 avec y0 = p2 / (2p) = ½p. Eméca = ½mv02 +½mgp en un point M (x,y) : Eméca = ½mv2 + mgy avec y = x2 / (2p) Eméca = ½mv2 + mgx2/(2p) ½mv02 +½mgp = ½mv2 + mgx2/(2p) v02+gp = v2 + gx2/p soit v2 = v02+gp -gx2/p (1). D'autre part en dérivant y par rapport au temps ( x est une fonction du temps) : y = x2 / (2p) donne y' = 2x x' / (2p) = x x'/p soit y'2 = x2 x'2 / p2 (2) vitesse v : v2 = x'2 + y'2. v02+gp -gx2/p = x'2 + x2 x'2 / p2 = x'2 [ 1+x2 / p2 ] en mulipliant par p2 :
x'2 =
[p2v02+gp3
-gpx2] / [ p2 +x2
].(3)
x'2 = 0= [p2v02+gp3 -gpx12] / [ p2 +x12 ]. p2v02+gp3 -gpx12=0 soit x12=(pv02+gp2) /g. or y1 = x12/ (2p) d'où y1= (v02+gp) /(2g). accélération : dériver x' et puis y' par rapport au temps (3) donne : 2x'x'' = [(-2gpxx')(p²+x²)-(p2v02+gp3 -gpx2)(2xx')] (p²+x²)-2. x'' =[(-gpx)(p²+x²)-(p2v02+gp3 -gpx2)(x)] (p²+x²)-2. [(-gpx)(p²+x²)-(p2v02+gp3 -gpx2)(x)] s'écrit : -gp3x-gpx3-p2v02x-gp3x +gpx3= -2gp3x-p2v02x x'' = -p2x(2gp+v02)(p²+x²)-2. y' = x x' / (p) soit y" = x'2/p +xx"/p or x'2 = [p2v02+gp3 -gpx2] [ p2 +x2 ]-1. y" = [pv02+gp2 -gpx2] [ p2 +x2 ]-1 -px2(2gp+v02)(p²+x²)-2 réduire au même dénominateur (p²+x²)2 y" =[(pv02+gp2 -gx2)(p²+x²)-px2(2gp+v02)](p²+x²)-2 (pv02+gp2 -gpx2)(p²+x²)-px2(2gp+v02) = p3v02+gp4 -gp2x2 + pv02x2+gp2x2 -gx4-2gp2x2-px2v02 = p3v02+gp4 -gx4-2gp2x2 d'où
y"=
(p3v02+gp4
-gx4-2gp2x2)(p²+x²)-2.
ce qui est écrit en bleu et en gras est un vecteur. La relation fondamentale de la dynamique s'acrit : mg + N = ma. soit Nx= mx" et Ny= m(y"+g) Nx= -mp2x(2gp+v02)(p²+x²)-2. Ny= m[(p3v02+gp4 -gx4-2gp2x2)(p²+x²)-2 +g] réduire au même dénominateur (p²+x²)2 : Ny= m[p3v02+gp4 -gx4-2gp2x2+gp4+gx4+2gp2x2](p²+x²)-2 Ny= m[p3v02+2gp4 ](p²+x²)-2 La composante Ny est toujours positive ; Nx est négative si x>0 et positive si x<0 : L'action du support N est donc orientée vers la concavité de la parabole et le contact est toujours réalisé.
retour - menu |