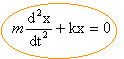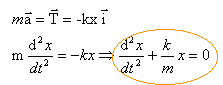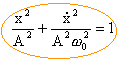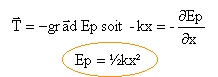|
Capes 96 exercice suivant : oscillateurs paramètriques |
||
|
||
|
On s'intéresse à quelques propriétés des oscillateurs à une dimension, c'est à dire dont l'évolution en fonction du temps peut être analysée par une fonction x(t). On appelle oscillateur harmonique tout système dont la fonction x(t) correspondante est solution de l'équation différentielle : 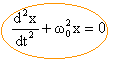 w0
rad/s,est la pulsation propre de l'oscillateur w0
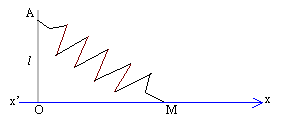
rad/s,est la pulsation propre de l'oscillateurle pendule élastique : 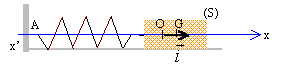 On considère un solide (S) de masse m, de centre d'inertie G. Quand S est immobile dans le référentiel dulaboratoire, G est en O, origine de l'axe horizontal x'x. Le solide S a pour seul mouvement possible une translation restiligne le long de l'axe x'x. S est soumis a une seule force, la tension T d'un ressort élastique de constante de raideur k, de masse négligeable. Il n'y a pas de frottement et le poids du solide est compensé par la réaction du support. La position de S est repérée par l'abscisse de G.
corrigé |
||
|
On applique le théorème du centre d'inertie , la seule force exercée sur S étant la tension du ressort.
avec w02= k/m fonction solution de cette équation différentielle : x(t) = A cos (w0 t + j) à t=0 : A =Acosj d'où cosj = 1 soit j = 0 x'(t) = -Aw0sin(w0 t) à t=0 x'(0) = 0 x(t) = A cos (w0 t ). plan des phases: x'(t) = -Aw0sin((w0 t) soit x'² =A²w²0sin²(w0 t)--> sin²(w0 t) = x'² /(A²w²0) x² = A² cos²(w0 t)-->cos²(w0 t) =x² / A² or cos²(w0 t) +sin²(w0 t) =1
la trajectoire dont l'équation est donnée
ci-dessus est, dans le plan des phases, une éllipse
de demi grand axe A et de demi petit axe Aw0.
La tension dérive d'une énergie potentielle; il existe une fonction Ep telle que :
l'origine de l'énergie potentielle élastique étant choisie à la position d'équilibre (G en O). En l'absence de frottement il y a conservation de l'énergie mécanique . E =½mv² +½kx² dériver par rapport au temps ( la dérivée de u² étant 2 uu') ½ m 2 v v' + ½ k 2 x x' = 0 avec v' = x" et x' = v en simplifiant par v, on retrouve : m x" + k x=0
|
||
|
Autres oscillateurs :
corrigé Le système physique n'a qu' un seul degré de liberté. Ecrire la conservation de l'énergie mécanique, puis dériver :on obtient une équation différentielle du second ordre de la forme x" = f(x, x'). Cette équation admet une solution unique pour des conditions initiales données. Développons Ep(x) au voisinage de la position d'équilibre x0: Ep(x) = Ep(x0) + (x-x0) (dEp / dx) x0 + ½(x-x0)² (d²Ep / dx²) x0 + ... F = - dEp / dx x0 est une position d'équilibre si F(x0) =0 soit (dEp / dx) x0 = 0 dériver Ep(x) pour étudier la stabilité de l'équilibre : F= - dEp/dx =-dEp / dx) x0- (x-x0) (d²Ep / dx²) x0= - (x-x0) (d²Ep / dx²) x0 si la dérivée seconde est positive, alors F est du signe opposé à x-x0 ; le point matériel est soumis à une force qui le ramène vers sa position d'équilibre x0. l'équilibre est dit "stable". Par contre
si la dérivée seconde est négative, le
point tend à s'éloigner de la position
d'équilibre et l'équilibre est dit "instable".
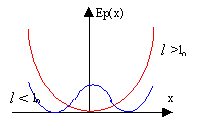
Ep(x)= ½ kDl²= ½k[ (l²+x²)½-l0]² dériver par rapport à x : dEp/dx= kx[1- l0(l²+x²)-½ ] si l >l0, la seule position d'équilibre est x=0 si l <l0, il y a trois positions d'équilibre: x=0; x = (l0²-l²)½; x = -(l0²-l²)½ l'allure de Ep est représentée ci-dessous:
stabilité de l'équilibre : pour x=0 : d²Ep/dx = k(1- l0/l) alors si l>l0 l'équilibre est stable. Si l<l0 l'équilibre est instable. pour x = (l0²-l²)½ ou x = -(l0²-l²)½ , d²Ep/dx =k((1- l²0/l²) positive; ces positions d'équilibre sont stables. Au voisinage
des positions d'équilibres stables, on a un
oscillateur harmonique.
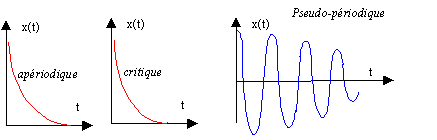
Les solutions de cette équation différentielle dépendent du signe du discriminant de l'équation caractéristique associée : D = l²-4km D <0 frottement faible, régime pseudo-périodique D =0, régime critique D >0, régime apériodique
la force de frottement visqueux n'est pas rigoureusement proportionnelle à la vitesse. La force de freinage par courant de Foucault est proportionnelle à la vitesse. l<0 : l'oscillateur reçoit de l'énergie. L'amplitude des oscillations augmente. |
||
|
|
||
|
pendule pesant : Il est constitué d'un solide de masse m et de centre de gravité G, mobile, sans frottement autour d'un axe horizontal D, perpendiculaire au plan de la figure. Le moment d'inertie du solide par rapport à cet axe est J 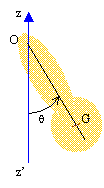
corrigé Le système étudié est le pendule ; référentiel du laboratoire supposé galiléen. Les forces agissant sur le système sont le poids et la réaction de l'axe. Le moment de la réaction de l'axe par rapport à O est nul. Le moment du poids par rapport à O est -mgOG sinq. Appliquer le théorème du moment cinétique par rapport à un axe fixe : Jd²q/dt² = -mgOG sinq. si l'angle est petit : sinq voisin de q radian. Jq" + mgOG q =0 q" + mgOG / J q =0 il s'agit de
l'équation différentielle d'un oscillateur
harmonique de pulsation propre [mgOG /
J]½.
|