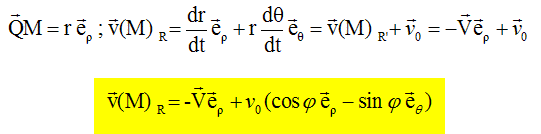Distance séparant deux oiseaux ; traversée d'une rivière

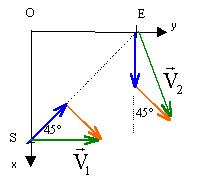
Deux oies situées initialement en E et S s'envolent au même instant, choisi comme origine des temps. ES=d. L'une se dirige vers E à la vitesse V0, l'autre se dirige plein sud à la vitesse V0. Les oies gardent le même cap durant tout le vol. Le vent souffle à vitesse constante V0 en direction du sud est (perpendiculairement à SE) 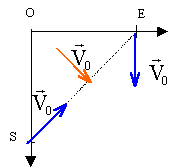- Exprimer en fonction du temps la distance séparant les deux oies. référentiel terrestre supposé galiléen Représentons les vecteurs vitesses par rapport au sol des deux oies à t=0 en tenant compte de la vitesse du vent. projections des deux vecteurs vitesses sur les axes: V1x = 0 ; V1y = V0 / cos 45 = 1,414 V0. V2x = V0 (1+ cos 45)= 1,707 V0 ; V2y = V0 cos 45 = 0,707 V0. les positions des oies sont des primitives des vitesses précédentes : oie S : x1 =0t + abscisse initiale = 0,707 d. y1 = 1,414 V0t + ordonnée initiale = 1,414 V0t oie E : x2 = 1,707 V0 t + abscisse initiale = 1,707 V0 t . y2 = 0,707 V0t + ordonnée initiale = 0,707 V0t +0,707 d.   distance D séparant les oies à la date t : D² = (x1-x2)² + (y1-y2)² après avoir effectué et simplifié : D² = 3,414V0² t² - 3,414 V0dt + d². - Quelle est la distance minimale ? A quelle date cette distance est elle minimale ? cette distance sera minimale( ou maximale) lorsque la dérivée par rapport au temps s'annule : D = [3,414V0² t² - 3,414 V0dt + d²)½. la dérivée de un est nu(n-1) u' avec n=½ et u = 3,414V0² t² - 3,414 V0dt + d² u' = 6,828 V0²t -3,414 V0d D' = ½ u -½ u' la dérivée s'annule pour t= d / (2V0) la dérivée est négative si t < d/ (2V0) et positive si t > d/ (2V0), il s'agit donc d'un minimum. repport de t = d / (2V0) dans D² ci-dessus Dmini = 0,38 d.   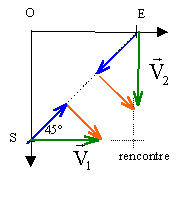Web www.chimix.com - Quelle doit être la vitesse de l'oiseau E, afin que les oies se rencontrent à la date calculée précédemment. vitesse de l'oie E pour que les oiseaux se rencontrent à t = d/ (2V0) l'oie S est au point de la rencontre : x1 = 0,707 d y1 = 1,414 V0t = 1,414 V0*d /(2V0) =0,707 d l'oie E est au point de la rencontre : x2 = x1 = Vx t = Vx d/ (2V0)=0,707 d d'où Vx = 1,414V0. y2 = y1 = Vy t + 0,707 d = Vy d/ (2V0) + 0,707 d= 0,707 d d'où Vy = 0 Le cap de l'oiseau sera de E vers S et sa vitesse V0. 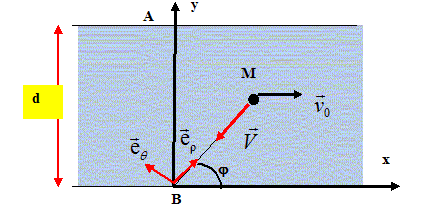Traversée d'une rivière. Un chien quitte le point A, situé sur la rive, et se dirige vers son maître, situé en B ; A et B sont directement opposés. La vitesse V du chien a un module constant et est toujours dirigée vers B. La vitesse v0 du courant est constante, parallèle aux rives.   Quelle est la trajectoire du chien ? R : référentiel lié à la berge de la rivière, associé aux coordonnées polaires er et eq. R' : référentiel lié au chien. Par suite : dr dt = -V + v0 cos j ; r dj dt = - v0 sin j Propriété d'une fonction composée : dr dt = dr dq dj dt =-V + v0 cos j = - v0 sin j r dr dj Séparation des variables : dr r = V - v0 cos j v0 sin j dj = Vdj v0 sin j - dj tanj Par intégration, il vient : ln r = V ln (tan ½j) v0 - ln (sin j) + ln Constante r = Constante sin j [ tan ½j] V/v0. Exprimer tan ½j en fonction de sin j et cos j : tan ½j = sin j 1 +cos j r = Constante sin j [ sin j 1 +cos j ]V/v0. La constante est déterminée par les conditions initiales : j(0) = ½p et r (0) = d : r = d sin j [ sin j 1 +cos j ]V/v0.

retour -menu