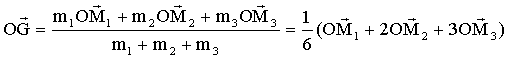Aurélie nov 2001
quantité de mouvement

référentiel barycentrique

Google

Les vecteurs sont écrits en gras et en bleu

On considère les points matériels de masses respectives m1 = 1 kg, m2 = 2 kg , m3 = 3 kg . Repère (O, i, j, k). ( référentiel galiléen) . Leurs coordonnées sont :

M1 (2t ; 3t² ; 1) ; M2 ( t²-1 ; -t ; 2t ) ; M3 ( -2 ; t-1 ; 1-t²)

  1. Donner l'expression littérale de la quantité de mouvement du système dans R.
  2. Quelles sont les coordonnées du centre de masse G des trois points matériels ainsi que celles de son vecteur vitesse dans R.
  3. Quelle est l'expression du vecteur quantité de mouvement de G dans R.
  4. On considère le référentiel barycentrique noté R*; repère associé(G, i, j, k). Exprimer les vitesses relatives des points matériels dans ce référentiel.
    - Calculer la quantité de mouvement du système dans R*. Conclure.
corrigé
vitesse des points matériels :

le vecteur vitesse vi est la dérivée du vecteur position OMi par rapport au temps.

OM1 ( 2t ; 3t² ; 1) donc v1 ( 2 ; 6t ; 0 )

OM2 ( t²-1 ; -t ; 2t) donc v2 ( 2t ; -1 ; 2 )

OM3 ( -2 ; t-1 ; 1-t²) donc v3 ( 0 ; 1 ; -2t )

vecteur quantité de mouvement du système de points :

pS = m1v1 +m2v2 +m3v3 = v1 + 2 v2 +3v3 .

suivant l'axe i : 2 +2*2t-3*0 = 2(1+2t)

suivant l'axe j : 6t-2 +3 = 6t+1

suivant l'axe k : 0+ 2*2+3*(-2t) = 2(2-3t)

pS [ 2(1+2t) ; 6t+1 ; 2(2-3t) ]

barycentre G :

OM1 ( 2t ; 3t² ; 1) ; OM2 ( t²-1 ; -t ; 2t) ; OM3 ( -2 ; t-1 ; 1-t²)

suivant i : 1/6( 2t +2(t²-1) +3(-2) ) soit 1/6 ( 2t² +2t-8)

suivantj : 1/6( 3t² +2(-t) +3(t-1) ) soit 1/6 ( 3t² + t -3)

suivant k : 1/6( 1 +2(2t) +3(1-t²) ) soit 1/6 ( -3t² +4t+4)

OG : 1/6( 2t² +2t-8 ; 3t² + t -3 ; -3t² +4t+4)

le vecteur vitesse v du centre d'inertie est la dérivée par rapport au temps du vecteur OG :

vG : 1/6 ( 4t+2 ; 6t+1 ; -6t+4 )
vecteur quantité de mouvement du centre de masse dans R :

pG = M vG avec M= m1 + m2 + m3 = 6 kg

pG : ( 4t+2 ; 6t+1 ; -6t+4 )

référentiel barycentrique R* :

vG : 1/6 ( 4t+2 ; 6t+1 ; -6t+4 ) et v1 ( 2 ; 6t ; 0 )

sur l'axe i ( 2-2/3t -1/3) soit (5/3 - 2/3 t )
v1* :

sur l'axe j ( 6t -t-1/6) soit (5t-1/6)

sur l'axe k ( t -2/3)

vG : 1/6 ( 4t+2 ; 6t+1 ; -6t+4 ) et v2 ( 2t ; -1 ; 2 )

sur l'axe i ( 2t-2/3t -1/3) soit (-1/3+ 4/3 t )
v2* :

sur l'axe j ( -1 -t-1/6) soit (-t-7/6)

sur l'axe k ( 2+ t -2/3) soit ( t +4/3)

vG : 1/6 ( 4t+2 ; 6t+1 ; -6t+4 ) et v3 ( 0 ; 1 ; -2t )

sur l'axe i ( 0-2/3t -1/3) soit (-1/3-2/3 t )
v3* :

sur l'axe j ( 1 -t-1/6) soit (-t+5/6)

sur l'axe k ( -2t + t -2/3) soit ( -t -2/3)
vecteur quantité de mouvement du système de points dans le référentiel barycentrique R* :

pS* = m1v1* +m2v2* +m3v3* = v1* + 2 v2* +3v3* .

suivant l'axe i : 5/3 - 2/3 t +2(4/3 t -1/3) +3 ( -2/3 t-1/3 ) = 0

suivant l'axe j : 5t-1/6 +2(-t-7/6) +3 (-t+5/6) = 0

suivant l'axe k : t-2/3 +2(t+4/3 ) +3 (-t-2/3) = 0

le vecteur quantité de mouvement du système de points est nul dans le référentiel barycentrique

retour - menu