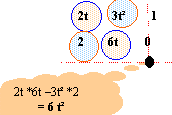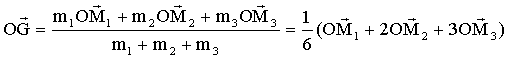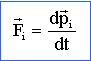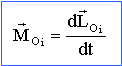Aurélie nov 2001
moment cinétique

théorème de Koënig

Google

Les vecteurs sont écrits en gras et en bleu

On considère les points matériels de masses respectives m1 = 1 kg; m2 = 2 kg , m3 = 3 kg ; repère galiléen (O, i, j, k). Leurs coordonnées sont :

M1 (2t ; 3t² ; 1) ; M2 ( t²-1 ; -t ; 2t ) ; M3 ( -2 ; t-1 ; 1-t²)

  1. Calculer les moments cinétiques en O des trois points matériels ainsi que celui du système.
  2. Appliquer le théorème de Koënig pour en déduire le moment cinétique L* dans le référentiel barycentrique.
  3. Donner les expressions littérales des forces F1, F2, F3 agissant respectivement sur chaque point ; exprimer F résultante des forces appliquée au système.
  4. Déterminer le moment en O des forces F1, F2, F3 et F.
corrigé
Calcul des moments cinétiques en O point de l'espace galiléen:

le vecteur vitesse vi est la dérivée du vecteur position OMi par rapport au temps.

OM1 ( 2t ; 3t² ; 1)
OM2 ( t²-1 ; -t ; 2t)
OM3 ( -2 ; t-1 ; 1-t²)
v1 ( 2 ; 6t ; 0 )
2 v2 : (4t ; -2 ; 4 )
3 v3 : 0 ; 3 ; -6t )
OM1 ^v1 ( -6t ; 2 ; 6t²)
OM2 ^ 2v2 ( 0 ; 4t²+4 ; 2t²+2)
OM3 ^ 3v3 ( -3t²+6t -3 ; -12t ; -6)
 

comment calculer un produit vectoriel ?

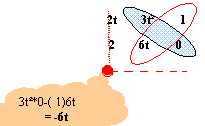
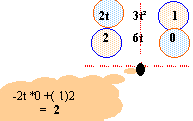
Le moment cinétique total en O du système de points est égal à la somme vectorielle des moments cinétiques en O des trois points composant le système.

LO = LO1 + LO2+ LO3

LO1 ( -6t ; 2 ; 6t²) ; LO2 ( 0 ; 4t²+4 ; 2t²+2) ; LO3 ( -3t²+6t -3 ; -12t ; -6)

suivant i : -6t +0 -3t² +6t -3 soit -3t² -3
LO :

suivant j : 2 + 4t² +4 -12t soit 4t²-12t + 6

suivant k : 6t² + 2t² +2 -6 soit 8t²-4

théorème de Koënig :

Dans le référentiel barycentrique R* le moment cinétique est indépendant du point par rapport auquel on le calcule; ce moment cinétique est noté L*.

Le moment cinétique d'un système de points calculé en un point O dans le référentiel R est égal à la somme vectorielle du moment cinétique en O de son centre de masse affecté de la masse totale du système et de son moment cinétique dans R*.

vitesse des points matériels :

le vecteur vitesse vi est la dérivée du vecteur position OMi par rapport au temps.

OM1 ( 2t ; 3t² ; 1) donc v1 ( 2 ; 6t ; 0 )

OM2 ( t²-1 ; -t ; 2t) donc v2 ( 2t ; -1 ; 2 )

OM3 ( -2 ; t-1 ; 1-t²) donc v3 ( 0 ; 1 ; -2t )

vecteur quantité de mouvement du système de points :

pS = m1v1 +m2v2 +m3v3 = v1 + 2 v2 +3v3 .

suivant l'axe i : 2 +2*2t-3*0 = 2(1+2t)

suivant l'axe j : 6t-2 +3 = 6t+1

suivant l'axe k : 0+ 2*2+3*(-2t) = 2(2-3t)

pS [ 2(1+2t) ; 6t+1 ; 2(2-3t) ]
barycentre G :

OM1 ( 2t ; 3t² ; 1) ; OM2 ( t²-1 ; -t ; 2t) ; OM3 ( -2 ; t-1 ; 1-t²)

suivant i : 1/6( 2t +2(t²-1) +3(-2) ) soit 1/6 ( 2t² +2t-8)

suivantj : 1/6( 3t² +2(-t) +3(t-1) ) soit 1/6 ( 3t² + t -3)

suivant k : 1/6( 1 +2(2t) +3(1-t²) ) soit 1/6 ( -3t² +4t+4)

OG : 1/6( 2t² +2t-8 ; 3t² + t -3 ; -3t² +4t+4)

OG
1/6( 2t² +2t-8)
1/6(3t² + t -3)
1/6(-3t² +4t+4)
pS
2(1+2t)
6t+1
2(2-3t)
OG^pS
1/6(-15t² -6t-16)
1/6(14t² -32t + 40)
1/6(4t² -36 t -2)
LO
-3t² -3
4t²-12t + 6
8t²-4
L* = LO - OG^pS
-½t² +t -1/3
1/3 ( 5t² -20t -2)
22/3 t²+6t -11/3

forces :

Pour chaque point , appliquer le principe fondamental de la dynamique

v1 ( 2 ; 6t ; 0 )
2 v2 ( 4t ; -2 ; 4 )
3 v3 ( 0 ; 3 ; -6t )
F1 (0 ; 6 ; 0)
F2 (4 ; 0 ; 0 )
F3 ( 0 ; 0 ; -6 )

F1 +F2 +F3 = F : (4 ; 6 ; -6 )

moments des forces en O :

appliquer le théorème du moment cinétique à chaque point matériel :

LO1 ( -6t ; 2 ; 6t²) ; LO2 ( 0 ; 4t²+4 ; 2t²+2) ; LO3 ( -3t²+6t -3 ; -12t ; -6)

LO1( -6t ; 2 ; 6t²)
LO2 ( 0 ; 4t²+4 ; 2t²+2)
LO3 ( -3t²+6t -3 ; -12t ; -6)
MO1( -6 ; 0 ; 12t)
MO2 ( 0 ; 8t ; 4t)
MO3( -6t+6 ; -12 ; 0)

le moment résultant est égal à la somme vectorielle des différents moments :

MO : ( -6t ; 8t-12 ; 16t )

autre méthode :

appliquer le théorème du moment cinétique au système pris dans sa totalité :

LO
-3t²-3
4t²-12t + 6
8t²-4
MO
-6t
8t-12
16t

retour - menu