Aurélie 02 /02
orbite de transfert dite de Hohmann

 

Google

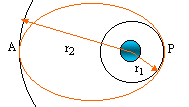
La mise en orbite d'un satellite géostationnaire s'accomplit en deux étapes : d'abord on place le satellite sur une orbite circulaire basse à l'altitude z1 ( r1 = Rterre + z1) puis on le fait passer sur l'orbite géostationnaire à l'altitude z2 ( r2 = Rterre + z2). Ce transit s'opère sur une orbite de transfert dite de Hohmann qui est elliptique. Le périgée P est sur l'orbite circulaire basse et l'apogée A est sur l'orbite géostationnaire. On utilise pour cela un petit réacteur qui émet en A et en P, pendant un temps très court, un jet de gaz donnant au satellite l'impulsion nécessaire.

  1. Donner les caractéristiques de la trajectoire du satellite géostationnaire. Quelles en sont les conséquences sur les deux autres trajectoires ?
  2. Exprimer en fonction de la masse de la terre M, de la masse du satellite m, de la constante de gravitation G, des rayons r1 et r2 :
    - l'énergie totale du satellite sur les trois orbites.
    - la variation d'énergie communiquée par le réacteur en P et en A.
    - Quelle est la durée du transit entre P et A ?
  3. En P (comme en A) il y a un brusque changement de vitesse noté Dv sans changement de position. Donner l'expression de la norme de cette variation de vitesse en fonction de G, M, r1 et r2 .
corrigé

géostationnaire : trajectoire circulaire dans le plan équatorial.

en conséquence les deux autres orbites sont situées dans le plan équatorial

l'énergie mécanique sur la trajectoire elliptique se conserve

aux points A et P : E = - GMm / (r1 +r2).

énergie mécanique sur l'orbite circulaire basse :

au point P : E1 = -½ mGM / r1

variation d'énergie mécanique en P :

DE = E -E1 = - GMm / (r1 +r2) + ½ mGM / r1

DE =GMm (r2 - r1) / [2(r1 +r2)r1].

DE est positive, la vitesse du satellite augmente.

énergie mécanique sur l'orbite circulaire haute :

au point A : E2 = -½ mGM / r2

variation d'énergie mécanique en A :

DE = E2 -E = - ½ mGM / r2 +GMm / (r1 +r2)

DE =GMm (r2 - r1) / [2(r1 +r2)r2].

durée du transfert :

le satellite parcourt la moitié de l'ellipse entre A et P. La durée du parcourt est la moitié de la période de révolution T sur l'ellipse. La troisiéme loi de kepler donne la période T en fonction de r1 et r2.

T² = 4p² / (GM) (r1 +r2)3.

norme de la variation de vitesse en P :

sur la nouvelle orbite circulaire la vitesse est v telle que : v² = GM/ r2.

sur l'orbite elliptique, avant l'impulsion du réacteur, l'énergie a pour expression :

E = - GMm/(r1 +r2) = ½ m(vA )² - GMm / r2.

vA ² = 2GM r1 / [(r1 +r2)r2] = 2 v² r1 / (r1 +r2)

vA / v = rac carrée [2 r1 / (r1 +r2)]

( v- vA ) / v = 1- rac carrée [2 r1 / (r1 +r2)].

retour - menu