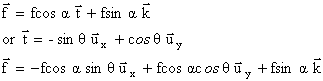Aurélie 01/02
un anneau glisse sur une hélice.

Google

Un anneau de masse m, de dimensions négligeables glisse de déplace sur une piste hélicoïdale circulaire d'axe Oz et dont les équations paramètriques sont : x = r cosq ; y = r sinq ; z= hq .

Les forces appliquées sont le poids, une force de frottement d'intensité constante f, colinéaire à la vitesse mais de sens contraire et une réaction de la piste normale au déplacement à chaque instant.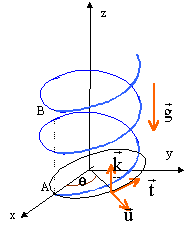

Dans un référentiel terrestre galiléen :

  1. Exprimer les composantes cartésiennes de la force de frottement en fonction de f, r, q et a angle entre la vitesse et le plan horizontal. Pour la suite on admettra que cet angle est constant et on exprimera tan a en fonction de h et r.
  2. Calculer le travail de la force de frottement lors du déplacement entre les points B (q =4p) et A (q=0).
  3. Exprimer en fonction des données le travail du poids et de la réaction de la piste entre B et A.
  4. En déduire la vitesse de l'anneau au point A sachant que sa vitesse initiale était nulle en B. Discuter.
corrigé
Dans le repère local (u, t, k) les composantes de la force de frottement sont :

(0 ; f cos a ; f sin a )

composante de la vitesse, dérivée du vecteur position par rapport au temps :

(-r sinq q ' ; r cosq q ' ; hq ' )

ou dans le repère local (u, t, k) :

(0, rq ' ; hq ' )

tan a = hq ' / (rq ') = h / r.

travail de la force de frottement :

déplacement élémentaire :

dx = -r sinq dq ; dy = r cosq dq ; dz = h dq ;

frottement (-f cosa sinq ; f cosa cosq ; f sina)

produit scalaire entre les vecteurs frottement et déplacement

-f r cosa sin²q dq + f r cosa cos²q + f h sina dq .

Pour obtenir le travail sur le déplacement B vers A, integrer entre 4p et 0, a et r sont constants

en remarquant que sin²q = ½(1-cos(2q)) et que cos²q = ½(1+cos(2q))

W = -4p f [r cosa + h sina].

travail du poids de B en A :

travail élémentaire au cours du déplacement élémentaire hdq :

dW = mghdq

Pour obtenir le travail sur le déplacement B vers A, integrer entre 4p et 0:

W = 4p mgh .

le travail de la réaction normale est nul ( force perpendiculaire au déplacement)

vitesse en A :

écrire le théorème de l'énergie cinétique entre B et A : (en B la vitesse est nulle)

½mv²A = 4p mgh -4p f [r cosa + h sina].

v²A =8p [gh - f /m[r cosa + h sina]].

cela est possible à condition que les frottements ne soient pas trop importants :

mgh>4p f [r cosa + h sina].

retour - menu