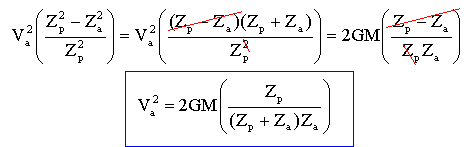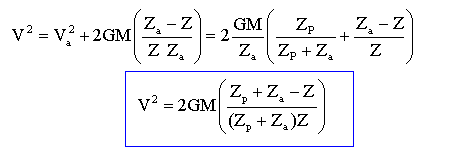Aurélie déc 2001
satellite sur une orbite elliptique

 

Google

Un satellite de la terre supposée sphérique et homogène a un apogée d'altitude L et un périgée d'altitude l. La terre a une masse M et un rayon R. G est la constante de gravitation.

  1. Quelle est la vitesse de ce satellite lorsqu'il passe à l'altitude z en fonction de M, G, R L, l et z
    G= 6,67 10-11 ; M =6 1024 kg ; R = 6,37 103 km ; L = 6500 km et l = 650 km.
  2. Calculer v dans les trois cas suivants : z = L ; z = l ; z = 3000 km
corrigé

 

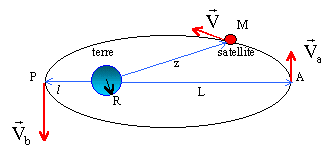
la force de gravitation est une force centrale, le moment cinétique se conserve

en particulier en A et P : on note Za = R+L et Zp = R+ l ; m : masse du satellite

m VaZa = mVpZp

VaZa = VpZp

Vp = VaZa / Zp.

conservation de l'énergie mécanique sur la trajectoire elliptique

aux points A et P : (M masse de la terre)

énergie potentielle : Ep(A) = - GmM/ Za et Ep(P)= - GmM/ Zp.

énergie cinétique : Ec(A) = ½mV²a et Ec(P) = ½mV²p.

½mV²a - GmM / Za = ½mV²p - GmM / Zp.

V²a - V²p = 2GM [ 1/ Za-1/Zp]

Remplacer Vp par l'expression ci dessus

V²a [1-(Za/Zp)²]= 2GM [ 1/ Za-1/Zp]

Au point M de l'ellipse à l'altitude z ; la vitesse est notée V ; R+z noté Z

½ mV² -GmM / Z = ½mV²a - GmM / Za

V² - V²a =2GM [ 1/ Z-1/Za]

Remplacer V²a par son expression et simplifier :

application numérique :

2GM= 2*6,67 10-11*6 1024 = 8 1014.

Za = (6370 + 6500) 103 = 1,287 107 m

Zp = (6370 + 650) 103 = 7,02 106 m

Zp +Za = 1,989 107 m

si Z = Za : V² = 8 1014*7,02 106 / ( 1,989 107*1,287 107) = 21,94 106.

V = 4,68 103 m/s

si Z = Zp : V² = 8 1014*1,287 107 / ( 1,989 107*7,02 106) = 0,737 108.

V = 8,58 103 m/s

si Z = 9,37 106 m : V² = 8 1014*(1,989 107-9,37 106) / ( 1,989 107*9,37 106) = 0,451 108.

V = 6,7 103 m/s

retour - menu