|
Capes 96 . |
||
|
||
corrigé |
||
|
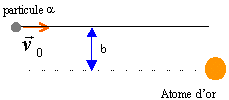
Rutherford en 1911 mit en évidence la présence d'un noyau dans les atomes à l'aide de l'expérience suivante: 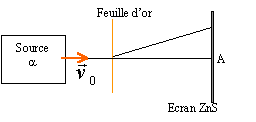 La traversée la feuille d'or par un projectile paraît impossible. Or la région A est illuminée de la même manière qu'en l'absence de feuille : la plupart des particules traversedonc la feuille F sans déviation.. L'atome a en conséquence une structure lacunaire. La trajectoire est une branche d'hyperbole
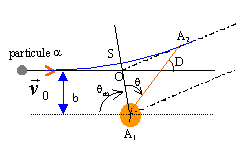
La masse réduiter est m = mM / (m+M) voisine de m si M>>m. paramètre d'impact : b = 2Ze² / (4pe0m tan(½F)v0²). b= 2*79*(1,6 10-19)² / [4*3,14*8,85 10-12*6,65 10-27 *tan30* 1,44 1014] b = 4,05 10-36 / 6,14 10-23= 6,59 10-14 m. Energie mécanique de la particule a située à l'infini : pas d'énergie potentielle; énergie cinétique : ½mv0². moment cinétique : s = mv0b particule a située au sommet de la trajectoire : la vitesse est perpendiculaire au rayon vecteur rm : le moment cinétique se conserve : s = mvSrm = mv0b l'énergie mécanique se conserve : ½mv0² = ½mv²S+ K / rm. avec K= 2Ze² /(4pe0) éliminer vS entre les deux relations ci-dessus. vS =v0b/ rm. ½mv0² = ½mv0²b²/r²m + K/ rm. r²m - 2K/(mv0²) rm -b²= 0 ou encore r²m - 2b tan(½F) rm -b²= 0 résoudre l'équation du second degré D= 4b²[tan²(½F) +1]=2b² / cos²(½F) rm = b tan(½F) +b/cos(½F) rm = 6,59 10-14 [tan30+1/cos30 ]= 1,14 10-13 m. On retrouve l'ordre de grandeur des dimensions du noyau 10-15 m ; l'atome ayant des dimensions voisines de 10-10 m.
retour - menu |