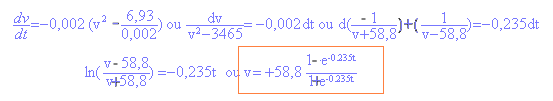Aurélie novembre 2000

équation différentielle et mécanique

  

Google

1

chute verticale et frottement

Une particule de masse m, de vitesse initiale v0, se déplace verticalement de haut en bas. La résistance de l'air, opposée à la vitesse, est proportionnelle à celle-ci telle que : f = - b.m.v , b étant une constante.

  1. Déterminer l' expression de la vitesse en fonction du temps.
  2. La vitesse limite de la particule.
  3. L'équation horaire exprimant le chemin parcouru z en fonction du temps.
  4. A quel instant la particule a-t-elle atteinte sa vitesse limite à 1% près ? Quelles sont alors son accélération et la distance parcourue ?

    Application numérique : g = 10 m.s-2 ; b = 25 s-1 ; v0 = 0,10 m.s-1 . 

corrigé

  

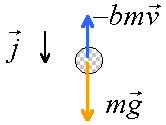
2ème loi de newton : projection sur un axe verticale orienté vers le bas

mg-bmv = ma = mv'

ou v'+bv = g (1)

vitesse limite atteinte, donc mouvement uniforme alors v'=0 et la vitesse limite est vl= g / b=0,4 ms-1.

il s'agit d'une solution particulière de l'équation (1).

v'+bv =0

solution générale : v =Cte exp(-bt)

 v'+bv = g

solution générale : v = Cte exp(-bt) +vl

à t=0 , v = v0 = Cte + vl d'où Cte = v0-vl = -0,3 ms-1.

v = -0,3 exp(-25t) + 0,4

altitude z : primitive de la vitesse

z = -0,3/(-25) exp(-25t) +0,4t + z0.

distance parcourue z0-z = 0,012 exp(-25t) +0,4t

la vitesse limite est atteinte à 1% près à la date :

(0,4-v) / 0,4 =0,01 = 0,3/0,4 exp(-25 t)

0,01= 0,75 exp (-25t) d'où t=0,17 s.

distance parcourue :0,012 exp (-25*0,17) +0,4 *0,17 = 0,0682 m.

l'accélération est nulle ( la résistance de l'air neutralise le poids)

et le mouvement est rectiligne uniforme dès que la vitesse limite est atteinte.
2

chute non verticale et frottement

 

  1. Un ballon de football, de masse m, tombant en chute libre, atteint la vitesse limite u = 18 m/s. En supposant la résistance de l'air de la forme f =-km v établir l'expression de k, et le calculer.
  2. Lors du dégagement , le gardien communique au ballon, depuis le sol, une vitesse initiale égale à 25 m/s, orientée à 45° vers le haut par rapport à l'horizontale. Etablir les équations du mouvement du ballon.
  3. Calculer la portée réelle du tir, et comparer à la valeur théoriquement déterminée en ignorant la résistance de l'air. 
corrigé

 

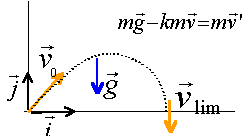
projections sur les 2 axes : v'x+kvx= 0 (1)

v'y+ kvy= -g (2)

doù la vitesse limite vly= -g / k et vlx=0

le signe moins signifie que vly est en sens contraire de l'axe.

la vitesse limite est atteinte lors de la descente du ballon.

k=9,8/18=0,544 s-1.

solution générale de (1) : vx= Cte exp(-kt)

à t=0, vx(t=0) = v0cos45 =25*0,707=17,67 ms-1.

vx= 17,67 exp(-kt)

solution générale de : v'y+ kvy=0

vy= Cte exp(-kt)

solution générale de (2) : vy= Cte exp(-kt) - 18

à t=0, vy(t=0) = v0cos45 =25*0,707=17,67 ms-1 d'où Cte= 35,67

vy= 35,67 exp(-kt) -18.

équations du mouvement : (primitive de la vitesse)

x = 17,67 / (-k) exp(-kt) + Cte = -32,48 exp(-0,544t) + Cte

à t=0, x=0 d'où Cte =32,48

x = 32,48 (1-exp(-0,544t))

y = 35,67/(-k) exp(-kt) - 18t + Cte = -65,57 exp(-0,544t) - 18t + Cte

à t=0, y=0 d'où Cte = 65,57

y = 65,57 (1-exp(-0,544t)) - 18t .

portée du tir : écrire que y = 0, contact avec le sol horizontal

en remarquant que la vitesse limite est atteinte ( le terme exp(-0,544t) est négligeable)

y = -18 t +65,57 soit t = 3,64 s

x = 32,48 m.

portée théorique sans frottement :v0² sin 2*45 /g = 63,7 m.

 
3

reccord de descente à ski

Un skieur de masse m = 80 kg glisse sans frottement sur une piste rectiligne faisant un angle a avec l'horizontale ( 45° ). Il subit de la part de l'air une force de résistance 0,5 k.S.v2 , où S = 0,40 m2 et k est le coefficient aérodynamique de valeur 0,80 S.I.. Ce skieur part sans vitesse initiale.

  1. Calculer la vitesse limite atteinte par ce skieur.
  2. Etablir la loi de vitesse en fonction du temps et faire l'application numérique. Quel temps faut-il au skieur pour atteindre la vitesse limite à 1 % près ?
  3. Le coefficient de frottement des skis sur la neige n'est plus nul mais vaut f = 0,05 . Quelle est la nouvelle vitesse limite ?
  4. Le record de vitesse à skis est-il un problème de glisse ou un problème d'aérodynamisme ?
corrigé

 

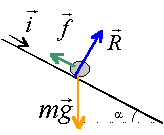
relation fondamentale de la dynamique suivant l'axe i :

mgsina - 0,5kSv2 = mv'

ou v' + 0,5kS/m v2 =gsina

v'+0,002 v2 = 6,93 (1)

vitesse limite : mgsina = 0,5kSv2

v2= 2mgsina / (kS) = 3464,3

vlim =58,85 ms-1.solution particulière de (1)

solution générale de (1):

durée au bout de laquelle la vitesse atteint la vitesse limite à 1% près. 

 on trouve t =22,5 s

mgsina - 0,5kSv2 -f = mv'

v' + 0,5kS/m v2 =gsina + f / m

le terme f / m est négligeable devant gsina.

la vitesse limite est d'abord un problème d'aérodynamisme.

retour - menu