|
|
chute de
la terre sur le soleil
|
|
|
|
|
1
rappels
mathématiques
|
On considère l'intégrale suivante :
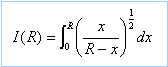
- Si x et R ont les dimensions d'une longueur,
quelle est la dimension de I ? Calculer I en effectuant
le changement de variable x=cos²q.
corrigé
|
|
|
|
|
2
gravitation
|
On suppose que le mouvement de la terre de masse m autour
du soleil est un mouvement circulaire uniforme de rayon R,
de vitesse v0. Terre et Soleil sont
assimilés à des points matériels.
- Donnez l'expression de la force exercée par le
soleil sur la terre ainsi que l'expression de la vitesse
v0 en fonction de Ms et /ou m , de la
constante de gravitation G et de R.
corrigé
|
|
|
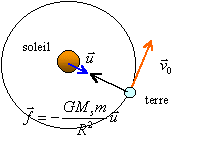
l'accélération est centripète de
norme aN= v0² / R
la seconde loi de newton s'écrit :
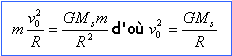
|
|
3
aspect
énergétique de la chute
|
On imagine que la vitesse de la terre s'annule
brusquement. Celle ci soumise uniquement à la force
de gravitation exercée par le soleil va donc finir
par tomber sur le soleil. La terre décrit une
trajectoire rectiligne et on se propose de déterminer
la durée de la chute, tout frottement étant
négligé.
- Exprimer l'énergie cinétique de la
terre lorsque celle ci se trouve à la distance x
du soleil.
- L'énergie potentielle de la terre dans le
champ de gravitation du soleil est de la forme
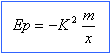 où
K est une constante positive. Exprimer l'énergie
mécanique de la terre. où
K est une constante positive. Exprimer l'énergie
mécanique de la terre.
corrigé
|
|
|
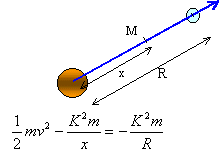
|
|
4
équation
différentielle et son
intégration
|
- En déduire que l'équation
différentielle qui régit la chute est du
type dt=g(x) dx où g(x) est une fonction de x que
l'on précisera.
- Intégrer cette équation
différentielle et montrer que le temps de chute
Tc ne dépend que de K et R.
- K peut se mettre sous la forme K=
Ga
Msb. A
partir d'une analyse dimentionnelle en déduire
a et
b.
- Calculer Tc en jours.
corrigé
|
|
|
à partir de l'expression ci dessus (question
3)
- diviser chaque terme par la masse m
- faire passer les termes d'énergie potentielle
à droite du signe égal
- réduire au même dénominateur
- prendre la racine carrée de chaque membre
- la vitesse est la dérivée de l'abscisse
x par rapport au temps
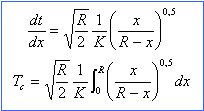
retour
- menu
|
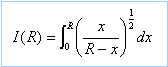

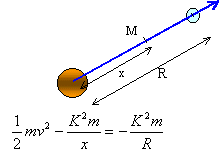
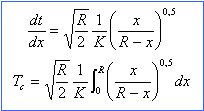
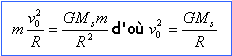
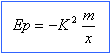 où
K est une constante positive. Exprimer l'énergie
mécanique de la terre.
où
K est une constante positive. Exprimer l'énergie
mécanique de la terre.