|
|
|||
|
|||
|
énergie trajectoire parabolique
|
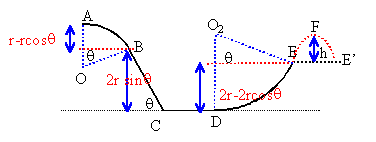
Un chariot de masse m=200g, de dimension négligeable, est mobile sans frottement sur une piste situé dans le plan vertical. On prendra g=10m.s-2 . La piste est formée de plusieurs parties AB partie circulaire de centre 0 et de rayon r constant et d'angle q =AOB variable. BC partie rectiligne de longueur 2r se raccordant tangentiellement à AB CD partie rectiligne de longueur r DE circonférence de rayon 2r, de centre O2 et raccordé tangentiellement à CD avec q =DO2E La piste est interrompue entre E et E' , situés dans une même plan horizontal; le chariot décrit alors une parabole ESE' de sommet S qui se raccorde à la piste en E et E', puis la piste E'F. 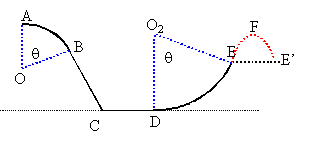
corrigé |
||
|
hB= 2r sinq ; hA= 2r sinq + r(1-cosq) ; hE= 2r(1-cosq ) énergies : en A l'énergie mécanique est sous forme potentielle de pesanteur : mghA. en B, l'énergie mécanique est sous forme cinétique et potentielle de pesanteur : ½ mv²B + mg hB. en C et en D, l'énergie mécanique est sous forme cinétique: ½mv²C = ½mv²D. en E l'énergie mécanique est sous forme cinétique et potentielle de pesanteur ½ mv²E + mg hE. l'action du support perpendiculaire à la vitesse ne travaille pas; seul le poids travaille et l'énergie mécanique se conserve. mghA =½ mv²B + mg hB. v²B = 2g(hA -hB) = 2g r(1-cosq) d'où vB= 3,13 m/s ( en supposant que le solide n'a pas quité la piste en B) v²C = 2ghA = 2g r(1+2sinq-cosq) d'où vC= 6,6 m/s v²E = v ²C - 2ghE = 2g r(1+2sinq-cosq) - 2g r(2-2cosq) =2gr(-1+2sinq+cosq) d'où vE= 4,9 m/s réaction du support:
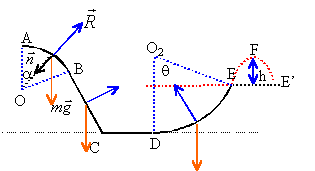
sur l'arc AB : relation fondamentale de la dynamique suivant l'axe n de la base de Frenet -R+mg cos a = mv²/r R= m(g cos a -v²/r) avec v²= 2gr (hA-h) = 2gr(1-cosa) R= mg(3cosa-2) on quitte le support et on décolle si R=0 soit cosa = 2/3 et a = 48,18° en conséquence le point B n'est pas atteint (q=60° supérieur à 48,18°) sur le plan BC : relation fondamentale de la dynamique suivant un axe perpendiculaire au plan R-mgcosq = 0 d'où R= 0,2*10*cos60 = 1 N (pas de décollage, le solide reste sur le plan donc pas d'accélération suivant la normale au plan) sur l'arc DE ( en E): relation fondamentale de la dynamique suivant l'axe n de la base de Frenet R-mg cos q = mv²E/(2r)=mg(-1+2sinq+cosq) R= mg(-1+2sinq+2cosq) = 0,2*10(-1+1,732+1)= 3,4 N mouvement parabolique : au sommet S, la composante verticale de la vitesse est nulle. la composante horizontale de la vitesse vaut vEcosq. énergie cinétique : ½ m (vEcosq)² énergie potentielle de pesanteur : mghS=mg(h+hE) l'énergie mécanique se conserve entre E et S: ½ m (vEcosq)²+mg(h+hE) = ½mv²E+mghE. ½ mv²E-½ m (vEcosq)² = mgh ½ (vEsinq)² =gh distance EE': 2 fois l'abscisse du point S du fait de la symétrie de la parabole au point S, la composante verticale de la vitesse est nulle: vEsinq-gt=0 d'où t = vEsinq/g abscisse de S : xS= vEcosq t = vEcosq vEsinq/g = vE²sinq cosq /g EE'= 2vE²sinq cosq /g = 2 (vEsinq)² cosq /(g sinq) = 4ghcosq /(g sinq) =4 h cotan q.
force de frottement entre C et D: l'énergie mécanique est sous forme cinétique en C: ½ mv²C. entre C et D, poids et action du support, perpendiculaires à la vitesse ne travaillent pas. seule la force de frottement travaille : -f r th de l'énergie cinétique entre C et D : 0-½ mv²C= -f r f = ½ mv²C/r = mg(2 sinq + 1-cosq) = 0,2*10(1,732 +1-0,5) = 4,46 N |