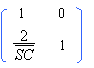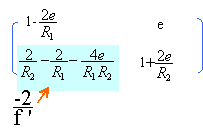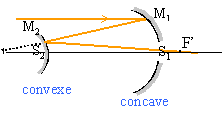
1

objectif : miroir concave associé à un miroir convexe

L'objectif d'un télescope de type Cassegrain est constitué de deux miroirs sphériques : un miroir concave M1 de sommet S1, et de centre C1 et de foyer F1, appelé miroir primaire. un miroir convexe M2 de sommet S2, de centre C2 et de foyer F2, plus petit que M1, appelé miroir secondaire. Le miroir primaire M1 est percé en son sommet d'un trou de rayon a qui permet le passage de la lumière après deux réflexions, la première sur le miroir primaire et la deuxième sur le miroir secondaire. Dans la suite, on supposera que les centres C1 et C2 des deux miroirs sont confondus en C. Les rayons d'ouvertures des miroirs M1 et M2 sont respectivement a1 et a2. On se place dans les conditions de l'approximation de Gauss. Déterminez la position du foyer principal image F' de l'objectif Cassegrain ; on donnera l'expression de la mesure algébrique CF' en fonction de R1=CS1 et R2=CS2. Quelle relation existe-t-il entre R1 et R2 pour que le foyer principal image F' soit au sommet S1 de M1? On donne R2=0,4m ; déterminer R1. Determiner les relations de conjugaison de cet objectif ; par rapport à quel point a-t-on interêt à les exprimer et pourquoi? On considère un faisceau incident cylindrique parallèle à l'axe optique. Déterminer le rayon d'ouverture a2 en fonction de a1 pour que tout rayon réfléchi par M1 le soit ensuite par M2. A.N : a1=3cm, R1=0,4m Representer sur un graphique à l'echelle la forme du faisceau émergent.(échelle 1cm pour 10cm suivant l'axe optique et 1cm pour 1cm pour les directions transverses). On souhaite former avec cet objectif Cassegrain l'image d'étoiles dont la direction puisse faire un angle a de part et d'autre de l'axe optique. Quelles sont les valeurs maximales a max de alpha et a max de a, rayon du trou central du miroir primaire M1, pour que les rayons réfléchis successivement par M1 et M2 puissent traverser M1 sans qu'aucun rayon provenant d'une étoile puisse passer directement par le trou?  quelques idées... 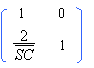matrice de transfert ou matrice de réflexion d'un miroir sphérique : matrice de transfert du télescope ( entre le sommet S1 du miroir primaire et le sommet du miroire secondaire S2 après réflexion). on note e la distance des 2 miroirs. 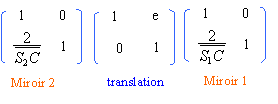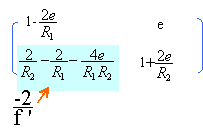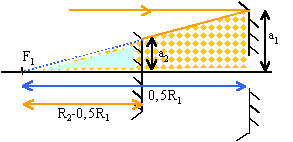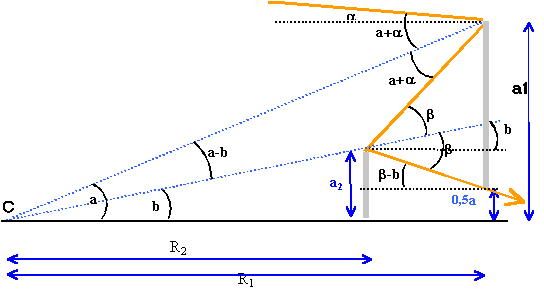e = R1-R2 avec mesure algébrique de S2C = R2 (miroir convexe divergent) et avec mesure algébrique de S1C =-R1 (miroir concave convergent) si F' est en S1, alors l'expression de la distance focale ci dessus est égale à 1 /R1 d'où R1=2R2 = 0,8 m les triangles hachurés ont des cotés proportionnels a1* (R2-0,5R1) = a2* (0,5R1) Une construction claire (nous avons un peu triché sur la construction des rayons lumineux)   retour - menu