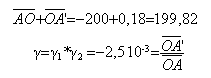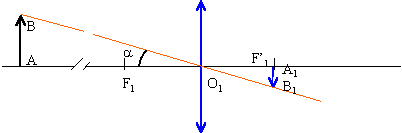
1

lentille convergente associée à une lentille divergente

Un téléobjectif est constitué de 2 lentilles minces dont les axes principaux coïncident. Les lentilles L1 et L2 ont pour vergences respectives C1=10d et C2= -40d. La distance O1O2 des centres optiques est 8 cm. Un objet AB de hauteur h= 0,75 m est placé à une distance d=200 m de O1 sur l'axe principal. Enoncer les conditions de Gauss relatives aux lentilles minces. Déterminer les caractéristiques de l'image A1B1 donnée par la première lentille. Quel rôle joue A1B1 pour la seconde lentille. Déterminer les caractéristiques de l'image A'B' donnée par la seconde lentille. Ces résultats(grandeur et nature de l'image) sont ils conformes aux propriétés de l'image que doit donner un téléobjectif sur la pellicule de l'appareil photographique ? Déterminer la position de la lentille convergente unique permettant d'arriver au même résultat. Quelle serait sa distance focale ? En comparant les grandeurs des images, montrer l'intérêt d'un téléobjectif par rapport à un objectif standard de distance focale 50 mm.   corrigé conditions de Gauss : conditions d'obtention de bonnes images objet de petites dimensions placés au voisinage de l'axe optique principal éliminer en diaphragmant les rayons trop inclinés sur l'axe optique principal distance focale = 1/ 10 =0,1 m l'objet placé à un distance de 200m, bien supérieure à la distance focale 0,1 m de la lentille est considéré à l'infini. L'image A1B1 se forme dans le plan focale image, image réelle, de sens contraire à l'objet. 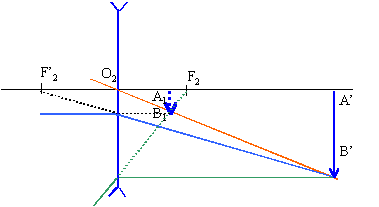calculs : tan a =0,75 /200 =0,00375 a =0,00375 radian A1B1 = 0,00375*10 = 0,0375 cm grandissement : g1 = 0,1 / (-200 ) = -5 10-4 A1B1 joue le rôle d'objet virtuel (placé derrière la seconde lentille) pour la seconde lentille.   mesure algébrique O2A1=0,02 m ; 1 / O2F'2= - 40 d. appliquer la formule de conjugaison : - 40 = -1 /0,02 +1/ mes.alg.O2A'2 d'où mes.alg.O2A'2 = 0,1 m grandissement g2 = mesure algébrique O2A'2 / mesure algébrique O2A1 g2 = 0,1 / 0,02 = 5 hauteur de l'image A'B' : 5*0,0375 =0,187 cm L'image sur la pellicule doit être réelle (ce qui est le cas ici). La dimension de l'image est par contre un peu trop petite. lentille convergente unique donnant le même résultat : La résolution de ce système donne la distance objet-lentille :199,32 m et la distance lentille-image 0,498m. appliquer la formule de conjugaison pour trouver la distance focale, avec : mes algébrique OA= -199,32 m et mes algébrique OA' =0,498 m d'où f =0,498 m. grandissement avec téléobjectif : -2,5 10-3. grandissement avec lentille unique de 50 mm de focale : objet à l'infini, image dans le plan focal image donc g'= 0,05 /(-200) =-2,5 10-4. soit une image 10 fois plus petite qu'avec le téléobjectif.   retour - menu