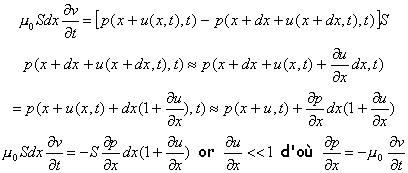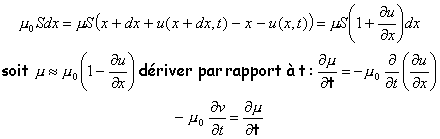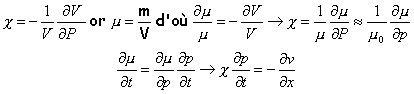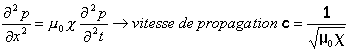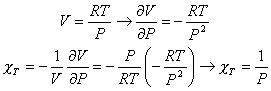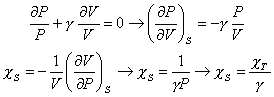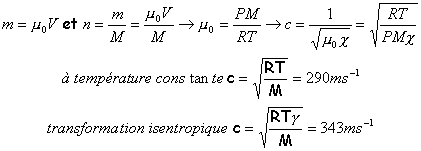notions de base

(quiz)

ondes électromagnétiques

ondes sur une corde

Ondes sonores se propageant dans un tuyau d'après Capes 94

Dans un tuyau de section S constante se propagent des ondes sonores caractérisées à l'abscisse x par :

 

1

équation d'onde vérifiée par la surpression
 

On s'intéresse au mouvement de l'air contenu dans une tranche élémentaire de tuyau comprise entre les abscisses x et x+dx

Déduire des relations ci dessus une équation d'onde vérifiée par la surpression p(x,t). Quelle est la vitesse de propagation de l'onde ?

corrigé

 

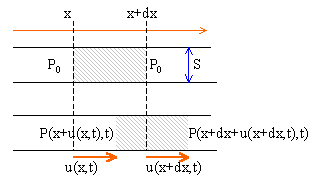
Appliquer la relation fondamentale de la dynamique à la tranche de fluide au repos comprise entre les abscisses x et x+dx. La masse de cette tranche est dm =m0Sdx. Au passage de l'onde sonore, la tranche se trouve entre les abscisses x+u(x,t) et x+dx+u(x+dx,t).

Projection de cette relation sur un axe horizontal :

conservation de la masse de gaz :

coefficient de compressibilité en fonction de la pression et de la masse volumique : 

dériver les équations obtenues précédemment respectivement par rapport à x et à t. On retrouve la forme générale d'une équation d'onde

 
2

transformation isentropique d'un gaz
 

 

La valeur du coefficient de compressibilité dépend de la transformation subie par le gaz. On définit cT coefficient isotherme et cS coefficient isentropique.

  1. Exprimer en fonction de la pression cT pour un gaz parfait.
  2. Donner l'équation d'une transformation isentropique et exprimer cS pour un gaz parfait.
  3. Exprimer dans les 2 cas envisagés ci dessus, la vitesse de propagation du son dans l'air en fonction de R (constante molaire des gaz parfaits), de M (masse molaire du gaz), de g= Cp/Cv et de la température T.
  4. Calculer cette vitesse .T=293 K; M=29 g mol-1 ; R=8,315 J mol-1 K-1.
corrigé

 

Equation des gaz parfaits pour une mole PV=RT. Dériver cette expression par rapport à P.

transformation isentropique PVg=Cte puis différencier :

expression de la vitesse de propagation des ondes :

retour - menu