_

interférences lycée - sup
1	définitions
le phénomène d' interférences Les interférences ne peuvent avoir lieu qu'entre deux ondes cohérentes. Dans la région où se superposent les ondes, l'intensité lumineuse passe par des maximums et des minimums qui peuvent être nuls. Les maximums dépassent la somme des intensités des faisceaux pris séparément. le dispositif interférentiel A partir d'une source ponctuelle et monochromatique, il suffit de diviser l'onde en deux sources secondaires. Ces 2 sources secondaires issues d'une même source sont cohérentes. interférences localisées ou non Les interférences sont non localisées si on les observe dans toute la région où les ondes se superposent. Dans le cas contraire, elles sont localisées. les conditions dobtention d'interférences Les ondes doivent être synchrones ( avoir même fréquence) Les ondes doivent être cohérentes. Les ondes doivent être à peu près parallèles.
2	dispositifs interférentiels
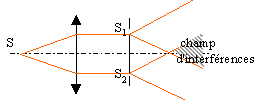
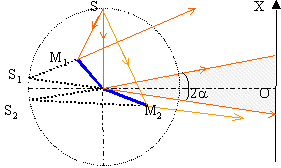
fentes (ou trous) d'Young : un écran opaque est percé de 2 fentes fines parallèles , très proches l'une de l'autre. La source monochromatique S est au foyer de la lentille (obtention d'un faisceau de lumière parallèle). miroirs de Fresnel : Une source ponctuelle éclaire 2 miroirs plans faisant entre eux un angle a de quelques minutes. Les rayons réfléchis qui semblent provenir des images S1 et S2 se rencontrent et les ondes qu'ils transportent interfèrent. Les franges sont des droites perpendiculaires au plan de la figure et à Ox.
3	quelques résultats
éclairement de l'écran E= E0 cos²( pp) ordre d'interférence p=d/l différence de marche d = n ax/D = n1 S1M - n2 S2M différence de phase F = 2pp interfrange i = l D/a abscisses des franges brillantes x = p i abscisses des franges noires x = (2p+1) i/2 longueur d'onde dans le milieu d'indice n l =l0/n Le chemin optique tient compte de l'indice , ce n'est pas le trajet suivi par la lumière
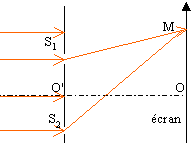
4	trous d'Young
O'S1=O'S2= a /2 ; O'O= D ; OM=x. La source de lumière est monochromatique de longueur d'onde l. Si D>>a l'éclairement de l'écran en M vaut : E= E0 cos²( pp) avec p=d/l ordre d'interférences et d = ax/D. Dans quel cas les interférences sont elles constructives ? Dans quel cas les interférences sont elles destructives ? Quel est la nature de l'ensemble des points pour lesquels l'éclairement est maxi ? calculer l'interfrange si D=1 m; 4 = 0,5 mm et l = 0,6 mm. corrigé Si l'ordre d'interférence est un entier ( la différence de marche est un multiple de la longueur d'onde), les interférences sont constructives ( franges brillantes : éclairement maximal). Si l'ordre d'interférence est égal à 2n+1 ( n entier) ( la différence de marche est un multiple impair de la demi longueur d'onde), les interférences sont destructives ( franges noires). Les franges brillantes sont des branches d'hyperboles. Etant donnée la faible étendue de la zone d'interférences les branches d'hyperboles sont assimilables à des segments de droites parallèles, perpendiculaires au plan de la feuille interfrange (i): distance séparant les milieux de deux franges consécutives de même nature. i = l D / a = 6 10-7 * 1 / 5 10-4 = 1,2 mm
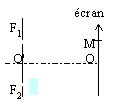
5	fentes d'Young et lame de verre
On place devant l'un des trous une lame de verre d'épaisseur e=0,01 mm , d'indice n=1,5 . D=O'O=1 m ; F1F2=0,5 mm et l = 0,6 mm. Déterminer de quelle distance et dans quel sens l'ensemble des franges s'est déplacé. Le dispositif est placé dans l'air d'indice n=1. corrigé En un point M de l'écran tel que OM=x, la différence de marche est : entre F2 et M le chemin optique est : absence de lame de verre : nairF2M présence de la lame : nair (F2M -e) + nverre e d1 = F2M -e + n e -F1M Or en l'absence de lame de verre d = F2M-F1M = ax / D d1 = ax / D + (n-1) e La frange centrale à l'abscisse x0 est telle que d1 = 0. x0 = - (n-1) e D/a L'ensemble du système de franges est déplacé du coté de la lame. x0 = (1,5-1)* 1 10-5 *1 / 5 10-4 = 1 cm
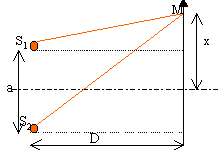
6 calculs de la différence de marche différence de marche d = n (S1M-S2M) . Tout le système est plongé dans le même milieu d'indice n. On supposera D >> a soit S1M + S2M voisin 2 D. 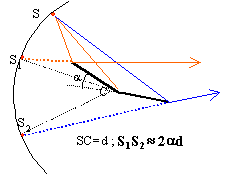S1M²=D²+(x-0,5 a)² S2M²=D²+(x+0,5 a)² S2M² -S1M² = (x+0,5 a)²-(x-0,5 a)² (S2M-S1M)(S1M+S2M) = 2 a x S2M-S1M voisin a x /D d = n a x /D miroirs de Fresnel remplacer a par 2a d ( a est l'angle des 2 miroirs ) dans la formule ci dessus S, S1, S2 sont sur le même cercle de centre C l'arc de cercle est égal à 2a d. Le segment S1S2 est à peu près confondu avec l'arc correspondant si l'angle est petit. 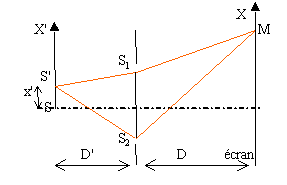7 déplacement de la source ponctuelle On déplace la source en S'. Le dispositif est placé dans un milieu d'indice n. On suppose D >> a et |x' | et D' D >> a et |x' | avec a=S1S2. La différence de marche en M est : d1 = n (S'S2+S2M-S'S1-S1M)= n(S'S2-S'S1) + n(S2M-S1M) d1 =n(S'S2-S'S1) + n a x /D un calcul comparable à celui du n°6 ci dessus conduit à S'S2-S'S1= a x' / D' d'où :d1 =n a (x' / D'+ x /D ) Les nouvelles franges brillantes sont telles que : n a (x' / D'+ x /D ) = p l0. x' / D'+ x /D = p l0 /(n a) ou x = p l D/a - Dx'/D' avec l =l0/n de même pour les franges noires : x = (2p+1) l D/(2a) - Dx'/D' L'interfrange reste inchangé. La nouvelle frange centrale a une abscisse X0= - Dx' / D' Tout le système de frange est déplacé en bloc du coté opposé au déplacement de la source. 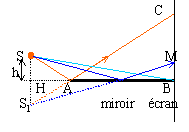8 miroir de Lloyd La lame de verre est éclairée sous une incidence rasante par une source ponctuelle monochromatique (h= 1 mm l= 0,546 mm SA=20 cm AB=10 cm) Sur l'écran on observe des franges d'interférences. Calculer l'interfrange, la largeur du champ d'interférences et le nombre d'interfranges corrigé Sur l'écran il se forme des interférences entre le faisceau issu directement de S et le faisceau réfléchi par le miroir. La différence de marche en un point M de l'écran, d'abscisse x est : d =SS1 x / HB + l /2 La réflexion entraîne une différence de marche supplémentaire de l /2, seule l'un des daisceau ayant subit une réflexion. Au point B x=0 et d = l /2 frange noire, la différence de marche étant un multiple impaire d'une demi longueur d'onde. interfrange i = l HB /SS1. i= 0,546 10-6*(0,1+0,2) / 2 10-3= 0,082 mm. le champ d'interférences est limité par le rayon SAC. BC / AB = HS1 / HA BC= 10-3*0,1 / 0,2 = 0,5 mm. 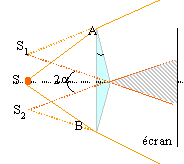le nombre d'interfranges est: 0,5 /0,082= 6,09 9 biprisme de Fresnel Deux prismes d'indice n d'angle A petit accolés à leur base forme un triangle isocèle. Ce biprisme est éclairé par un faisceau monochromatique ( l= 0,546 mm ; n=1,5 ; d=d'=1m ; A=10' =0,166° = 0,0029 radian). La source S est à une distance d du biprisme. L'écran est à une distance d' du biprisme. On observe des franges d'interférences. Calculer l'interfrange, la largeur du champ d'interférences et le nombre d'interfranges corrigé Les prismes ayant un angle A petit , la déviation provoquée par chaque prisme est : a=(n-1)A. Les 2 sources secondaires S1 et S2 images de S à travers les 2 prismes sont cohérentes. Dans la partie hachurée, les faisceaux provenant de S1 et S2 donnent des interférences. S1S2 =2a d ; D=d+d' interfrange i= l (d+d') / (2a d ) i= 0,546 10-6*2 /(2*(1,5-1)*0,0029*1) = 0,37 mm largeur du champ : 2a d' 2*(1,5-1)0,0029*1 = 3 mm nombre d'interfranges : 3/0,37= 8,1 9 franges brillantes et 8 franges noires, la frange centrale étant brillante.  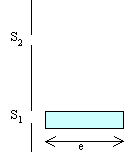10 mesure d'un indice de réfraction On considère le dispositif des fentes d'Young. Devant l'une des fentes on place un tube de verre (e= 2,5 cm de long ). La source est monochromatique ( l = 656,282 nm). De l'air (n=1,00029) sous pression normale, est placé dans le tube. Puis l'air est remplacé par un gaz inconnu dont on désire mesuré l'indice de réfraction. En un point de l'écran 22 franges défilent. Calculer l'indice du gaz. corrigé Au point M du champ d'interférences, la différence de marche est : lorsque le tube est rempli de gaz d'indice n : d1 =S1M-e+n e-S2M = d +(n-1)e = l D/a + (n-1) e lorsque le tube est rempli d'air d'indice na : d2 = l D/a + (na-1) e or 22 franges défilent :|d2 - d1 |= 22 l soit | na - n |= 22 l / e n étant plus grand que 1 : n = 1,00087   retour - menu