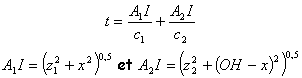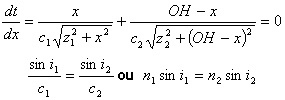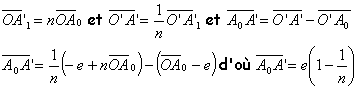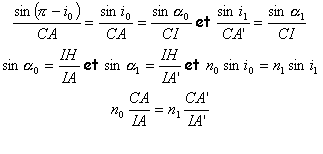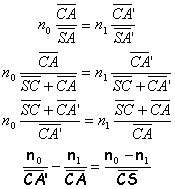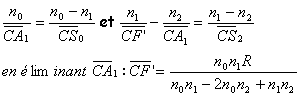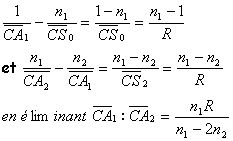|
optique géométrique - dioptre expression vectorielle de la loi de Snell-Descartes 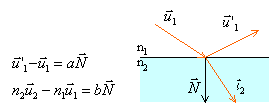
|
|
|
indice principe de Fermat |
|
|
|
Le chemin optique entre A et B
n'est pas la distance AB; il faut tenir compte de l'indice
de réfraction des milieux.
L'indice absolu de réfraction d'un milieu, noté n, est égal au rapport de la vitesse de la lumière dans le vide à la vitesse de la lumière dans le milieu considéré. Cet indice n est supérieur à 1. Le trajet suivi par la lumière entre 2 points A et B est tel que le chemin optique soit stationnaire par rapport aux trajets voisins allant de A à B. Dans la plupart des cas, cette condition implique que le chemin optique soit minimum. Le chemin optique devant être minimum, le trajet AB est une droite : les rayons lumineux sont donc rectilignes.
|
|
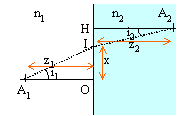
loi de Snell-Descartes |
|
|
durée du trajet entre A1 et A2 c1 vitesse de la lumière dans le milieu d'indice n1 et c2 dans le milieu d'indice n2.
le parcours A1IA2 est à durée minimale si dt / dx =0
|
|
|
approximation de Gauss |
|
|
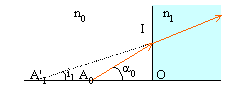
corrigé Un système optique est dit rigoureusement stigmatique pour un couple de points A0A'1 si tout rayon lumineux passant par A0 passe par A'1 après avoir traversé le système. Il y aura donc stigmatisme si OA'1 est indépendant de a0. 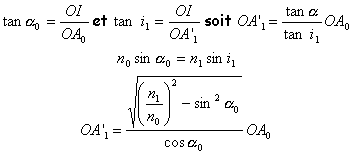
OA'1 dépend de l'angle a0. Le dioptre plan n'est pas stigmatique pour un couple de points quelconques. Le point A0 n'a pas d'image à travers le dioptre plan. L'approximation de Gauss consiste à considérer des rayons paraxiaux (angle d'incidence faible). Dans ce cas cos a0 voisin de 1 et sin a0 << n1 / n0. Il y a dans les conditions de Gauss stigmatisme approché; A'1 est l'image de A0, cette image est virtuelle ( située à gauche de la sortie du système optique). La relation ci dessus s'écrit alors : OA'1 = n1 / n0 OA0. |
|
|
lame à faces parallèles |
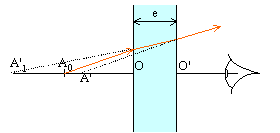
Etablir l'expression de la distance objet-image dans le cas du stigmatisme approché. Calculer cette distance si e=3 mm et n=1,5 (indice de la lame) . L'autre milieu est l'air. |
|
corrigé Le premier dioptre donne une image A'1 de A0 et le second dioptre donne une image A' de A0.
La distance objet-image ne dépend pas de la position de l'objet par rapport au dioptre. De plus le rayon émergent est parallèle au rayon incident. application numérique : 1 mm |
|
|
dioptre sphérique |
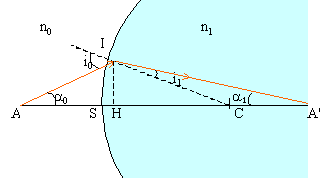
Montrer que n CA / IA est un invariant lorsque la lumière passe de A en A'. En déduire la relation de conjugaison du dioptre sphérique en prenant les origines au centre C. |
|
corrigé Dans les triangles ICA et ICA' :
Dans le cas de l'approximation de Gauss, les longueurs IA0 et IA1 peuvent être confondues avec SA0 et SA1.
|
|
|
boule |
Une boule homogène et isotrope, transparente sépare 2 milieux d'indice n1 et n2. 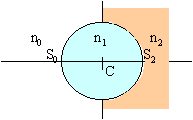
application numérique : R=S0C= 3 mm; n0=n2=1; n1=1,5 |
|
corrigé Le foyer image d'un système optique est le point conjugué du point du milieu objet situé à l'infini sur l'axe principal. La boule est constituée de 2 dioptres sphériques. Nous cherchons le conjugué d'un point sur l'axe, à l'infini dans l'espace objet à travers les 2 dioptres. Appliquer 2 fois la formule ci dessus :
application numérique : CF' = 4,5 mm. |
|
|
lentille boule |
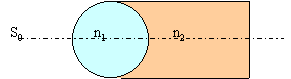
Une lentille boule (n1=3) assure le couplage lumineux entre unse jonction émettrice considérée comme ponctuelle placée en S0 et le milieu d'indice n2 =1,5 . Quelle est la nature du faisceau transmis dans ce milieu ? |
|
corrigé Cherchons quel est le conjugué de S0 à travers la lentille boule en appelant A1 l'image de S0 à travers le premier dioptre et A2 l'image définitive.
Les valeurs des indices sont telles que CA2 tend vers l'infini. Le faisceau transmis dans le milieuu d'indice n2 est un faisceau parallèle à l'axe optique. |