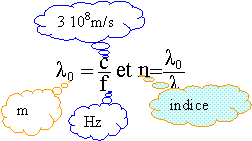1

optique géométrique

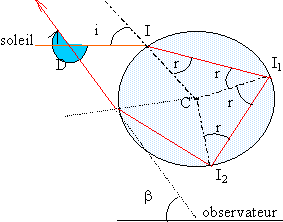
L'arc-en-ciel naît des réflexions et réfractions de la lumière du soleil à travers les gouttes d'eau dans les nuages. On représente une goutte d'eau par une sphère d'indice n = 1,33. L'observateur voit l'ensemble des lumières réémises par toutes les gouttes constituant le nuage. 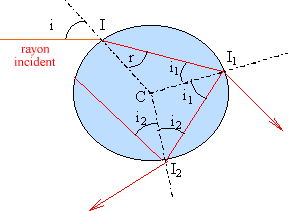On ne considère que la formation des deux premiers arcs correspondant aux rayons transmis après une ou deux réflexions à l'intérieur de la goutte. Pour simplifier l'étude on supposera travailler en lumière monochromatique.  Questions de cours : - Enoncer les lois de Descartes concernant la réflexion et la réfraction. - Définir réflexion totale et angle limite de réfraction. - Que devient l'énergie après plusieurs réflexions dans la goutte. - Une source émet une radiation de fréquence f=6,67 1014 Hz. Quelle est sa longueur d'onde dans le vide et dans l'eau? On considère une seule réflexion dans la sphère. Quelle est la déviation D1 d'un rayon sortant?  - Calculer la déviation Dp d'un rayon ayant subit p réflexions. - Montrer que la déviation est minimale , Dmp pour i=i0 lorsque di/dr = p+1. - En déduire sin i0 : calculer i0 et Dpm pour p =1, 2, 3. Le soleil considéré comme une source ponctuelle (S) située à une hauteur angulaire a au dessus de l'horizon, éclaire une vaste zone de pluie. Sachant que l'intensité de la lumière émergeant de la goutte est maximale au minimum de déviation, expliquer la formation de l'arc-en-ciel lorsque la lumière est blanche. On admet que la variation de l'indice n avec la longueur d'onde l0 dans le vide satisfait la loi de Cauchy : n = n0 + C / l02; n0 et C sont des constantes positives. On observe souvent un second arc-en-ciel d'intensité plus faible et inversé par rapport au premier. Calculer b=D-p . Interpréter sa formation en considérant une seconde réflexion dans la goutte d'eau.     corrigé A l'interface entre deux milieux transparents d'indice n1 et n2 : rayons incident, réfléchi et réfracté sont dans le même plan d'incidence les angles de réflexion et d'incidence sont égaux angle d'incidence et de réfraction sont liés par la relation : n1 sin i1 = n2 sin i2. si n1 > n2 (milieu n°1 plus réfringent) , il existe un angle d'incidence limite a au dela duquel le rayon réfracté n'existe plus n1 sin a = n2. si i1 > a, toute l'énergie lumineuse est réfléchie dans le milieu n°1. L'énergie se partage inégalement entre les rayons réfracté et réfléchi. Au fur et à mesure des réflexions à l'intérieur de la goutte, l'énergie diminue. Au dela de 2 réflexions, le rayon n'est plus visible. dans le vide : l 0 = 3 108 / 6,67 1014 = 0,45 10-6 m = 0,45 mm. dans l'eau : l = 0,45 / 1,33 = 0,338 mm. 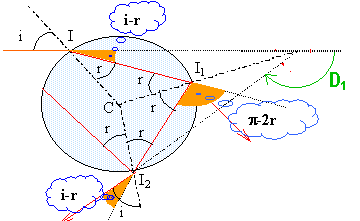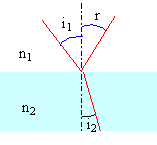En I et en I2, la réfraction entraîne une déviation : i-r En I1 la réflexion entraîne une déviation : p-2r soit au total : D1 = p+2i-4r. p réflexions entraînent une déviation : p(p-2r) Dp = pp-2(p+1)r + 2i dDp = -2(p+1) dr + 2di soit dDp / di = 2[1-(p+1) dr/di] passe par un mini ou un maxi si (p+1) dr = di de plus sin i = n sin r soit cos i di = n cos r dr ou dr/di = cos i / (n cos r) dDp / di = 2[ 1- (p+1) cos i / (n cos r)] or dD/ di est négatif pour i=0 et positif pour i= 90°: donc dD/ di passe par un minimum dDp / di =0 si (p+1) cos i0 = n cos r (p+1)² cos² i0 = n² cos² r et sin² i = n² sin² r d'où : (p+1)² - n² = [-1+(p+1)²]sin² i0. 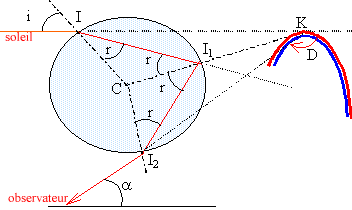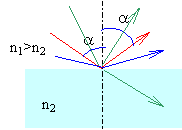p i0 r Dmp 1 59,6° 40,4° 138,4° 2 71,9° 45,6° 230,2 3 76,9° 47° 317,8° Pour une radiation déterminée, l'observateur reçoit les rayons qui semblent provenir d'un arc de cercle centré sur un axe défini par la position de l'observateur et la direction du rayon provenant du soleil. Lorsque la lumière est complexe chaque radiation donne son propre arc de cercle. Pour une valeur fixée de i, calculons da à partir de a = p-D = -2i +4r : da = 4 dr . Or sin i = n sinr donne : 0 = n cos r dr + sin r dn d'où dr = - tan r / n dn. Or n = n0 + C / l02; dn = -2C dl0 / l03. da = 8 C tan r dl0 / (nl03). Lorsque la longueur d'onde augmente, a augmente. Les différents arcs de cercles sont colorés du violet à l'intérieur, au rouge à l'extérieur. après une seconde réflexion dans la goutte : Dp = pp-2(p+1)r + 2i donne D = 2p-6r + 2i Pour une valeur fixée de i, calculons db à partir de b = D-p =p + 2i -6r : db = -6 dr . Or sin i = n sinr donne : 0 = n cos r dr + sin r dn d'où dr = - tan r / n dn. Or n = n0 + C / l02; dn = -2C dl0 / l03. db = -12 C tan r dl0 / (nl03). Lorsque la longueur d'onde augmente, b diminue. L'arc en ciel est bien inversé. retour - menu