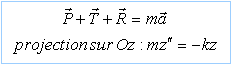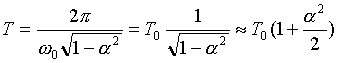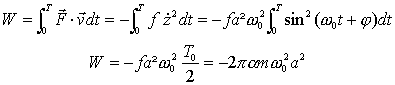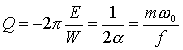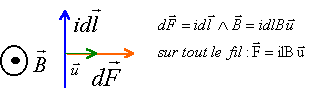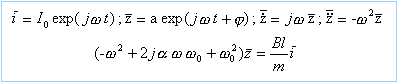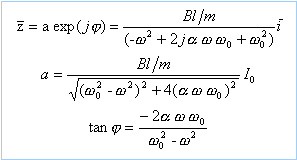|
|
||||||||||
|
||||||||||
|
oscillations libres |
La partie mécanique d'un haut parleur est constituée d'une membrane mobile, en forme de cône, solidaire d'un mandrin cylindrique sur lequel est enroulé le fil du bobinage. L'ensemble est maintenu en place par des suspensions élastiques qui jouent le rôle de guidage (le mouvement est limité à une translation de l'équipage mobile) . La partie mobile peut être représentée par une masse m, assimilable à un point matériel, mobile sans frottement sur une tige horizontale Oz. Elle est rappelée vers sa position d'équilibre (le point O) par un ressort de masse négligeable, de raideur k, pouvant travailler en extension comme en compression. On repère le point M par son abscisse z.
corrigé |
|||||||||
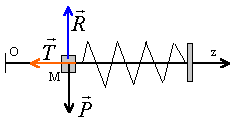
systéme étudié : la masse m; référentiel du laboratoire supposé galiléen. trois foces s'exercent sur le point M : le poids , la réaction du système de
quidage et la tension du ressort La relation fondamentale de la dynamique s'écrit :
L'équation différentielle est celle d'un oscillateur harmonique :
application numérique : w0=438,2 rad s-1; T0=14,3 ms ; N0=69,8 Hz
|
||||||||||
|
oscillations libres amorties |
.
corrigé |
|||||||||
|
l'équation caractéristique associée à l'équation différentielle s'écrit : m r²+f r+k = 0 La nature des solutions dépend du signe du discriminant D=f ²-4km Le régime critique correspond à D=0 soit fc²= 4km valeur numérique fc=7 kg s-1. L'équation différentielle s'écrit en remplaçant k/m par w0² et f par afc. z"+ 2aw0 z'+w0² z= 0 le discriminant réduit s'écrit : D'= w0² (a²-1)
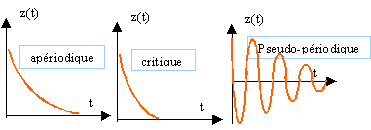
frottement faible a<1, les solutions de l'éqution différentielle sont de la forme :
à t=0 : z=z0 et z'=0 permettent de déterminer A et j.(A=z0et j=0) La pseudo-période est égale à : ( a très faible devant 1)
application numérique : T=14,3 ms l'écart relatif est a²/2 = 0,5% L'énergie de cet oscillateur est la somme de son énergie potentielle élastique ( énergie potentielle de pesanteur est constante, mouvement sur une horizontale) et de son énergie cinétique. E=0,5 mv²+0,5 kz² = 0,5 mw0²sin²(w0t+j)+0,5 ka²cos²(w0t+j) or k=mw0² d'où E=0,5 ka². travail de la force de frottement au cours d'une période :
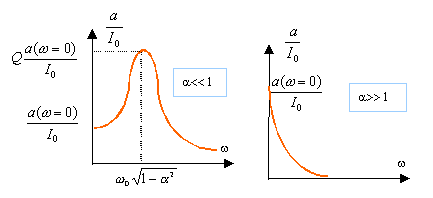
Expression du facteur de qualité Q de l'oscillateur :
|
||||||||||
|
oscillations forcées |
corrigé |
|||||||||
|
Il suffit d'ajouter la force de Laplace au autres forces mz"=-fz'-kz+ilB soit z"+ 2aw0 z'+w0² z = Bl/m I0cos(wt) La solution de l'équation différentielle sans second membre correspond au régime transitoire. Ce régime disparaît au bout d'un temps assez court, quelle que soit la valeur de a, pour faire place à un régime permanent La solution générale de l'équation différentielle est la somme de la solution générale de l'équation sans second membre et de la solution particulière acos(wt). Le régime permanent correspond au régime foré imposé par l'exitateur. solution de l'équation (méthode utilisant les nombres complexes).
On trouve :
|
||||||||||
|
étude énergétique |
|
|||||||||
|
l'équation électrique relative au circuit s'écrit :
multiplier la première par i et la seconde par v, puis ajouter :
ui : puissance reçue par le dipole ri² : puissance dissipée par effet joule 0,5 Li² : puissance stockée dans la bobine 0,5 mv²: énergie cinétique de l'équipage mobile fv² : puissance de la force de frottement 0,5 kz² : énergie potentielle élastique La puissance acoustique émise sur une demi sphère est égale à 2pI A 60 Hz, Pa=5 mW et à 200 Hz, Pa=50 mW. rendement : pa/ p=2,5 % à 60Hz et 6 % à 200 Hz. La puissance moyenne fournie par le générateur est égale à la somme de la puissance sonore rayonnée par la source et de la puissance perdue par effet joule. |