Aurélie mars 2001

amplificateur opérationnel

fiche de révision

Google

1

source de tension commandée par le courant

On considère le montage suivant avec deux amplificateurs opérationnels idéaux. Exprimer Vs en fonction de R1, R2, R3 et I0.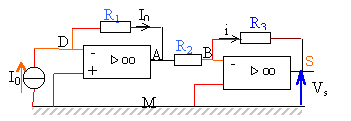

corrigé

B et d sont des masses virtuelles

UAM= UAD= - UDA =-R1I0.

Vs = USM = USB= - UBS = -R3 i

UAM= UAB donne -R1I0 = R2 i soit i =-R1 / R2I0 .

Vs =-R3 i = R3R1 / R2 I0 .

Source de tension commandée par le courant, dont l'impédance de sortie est celle du second amplificateur ( proche de zéro): cette source de tension est pratiquement idéale.
2

générateur de courant

L'amplificateur est considéré comme parfait et fonctionne en régime linéaire. Montrer que l'intensité du courant dans la branche AM est proportionnel à la différence V2-V1.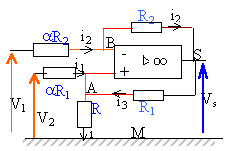

corrigé

A et B sont au même potentiel électrique donc USA=USB.

R2i2 = -R1i3.

V1 -aR2i2 = V2-aR1i1.

V2 -V1 = a(R1i1-R2i2) = a(R1i1+R1i3) =aR1 (i1+ i3)

or au noeud A : i = i1 + i3.

i = (V2 -V1) / (aR1 ).
3

comparateur

Dans le montage suivant, l'A.O fonctionne en comparateur; les courants d'entrée sont nuls et Us = m e avec m >>1. Exprimer Us en fonction de e, m, R et dR. Quel est le but de ce montage ?

remarque : dR <<R.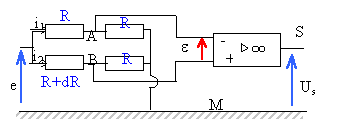

 

corrigé

e= 2Ri1 = (2R+dr)i2.

d'où i1 = e /(2R) et i2 = e / (2R+dR)

VA=Ri1 ;VB=Ri2 donne VA-VB= e = R(i1-i2)

remplacer i1 et i2 par leurs expressions en fonction de e.

e = R e[ 1/ (2R) -1 / (2R+dR)] R e dR / [2R(2R+dR)]

2RdR <<4R²

voisin de : e = e dR / (4R)

Us = me = m e dR / (4R).

Le gain en boucle ouverte m permet d'amplifier la tension de déséquilibre du pont et de détecter une petite variation de résistance.
4

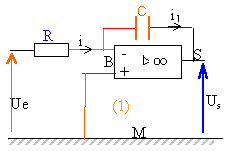
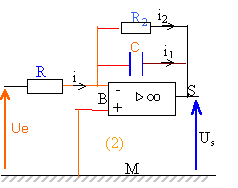
montage intégrateur

L'amplificateur opérationnel est idéal et fonctionne en régime linéaire. Initialement le condensateur est décharger. Ve est telle que Ve+E our t >=0 et Ve = 0 pour t<0.

  1. Montrer que le montage (1) est intégrateur.
  2. A quelle condition le montage (2) est-il intégrateur.
corrigé

montage (1) :

B est une masse virtuelle donc Ue= Ri et Us = -Q / C

i = dQ/dt = -C dUs/dt

Ue = -RC dUs/ dt

montage (2) :

Ue = R i ou i = Ue/R

Us = -R2 i2 ou i2 = -Us/R2.

i1 = i - i2 = Ue/R + Us/R2

autre expression de i1 :

Us = -Q/C ou dUs/dt = -1/C dQ/dt =-1/C i1.

Ue/R + Us/R2 = -CdUs/dt

pour t>0 : Us' +Us / (R2C) = -E / (RC)

solution générale de l'équation sans second membre : Us = A exp [-t / (R2C)]

solution particulière de l'équation différentielle : Us = cte = -ER2 / R.

solution générale de l'équation différentielle : Us = A exp [-t / (R2C)] -ER2 / R.

déterminer A d'après les conditions initiales, Q=0 :

0 = A -ER2 / R.

Us = ER2 / R{ exp [-t / (R2C)] -1}.

condition pour avoir un intégrateur:

t<<R2C soit exp [-t / (R2C)]= 1-t / (R2C) au premier ordre

Us = -E / (RC) t, primitive de E au coefficient -1/(RC près)

retour - menu