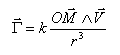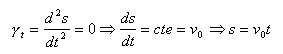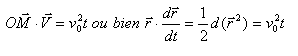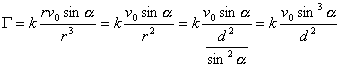Aurélie nov2000

accélération, vitesse , trajectoire

Google

1

accélération connue, étude de la trajectoire

On etudie le mouvement d'un point M dont le vecteur accélération est:

  1. où k est une constante positive donnée, O un point fixe, V le vecteur vitesse de M, r la distance OM supposée non nulle. A l'instant initial, le vecteur vitesse V0 est perpendiculaire à OM0. On pose d=OM0 valeur initiale de r.

  2. Exprimer en fonction de t l'abcisse curviligne de M sur sa trajectoire en prenant pour origine la position initiale et pour sens positif le sens défini par la croissance de t.
  3. Calculer la dérivée par rapport à t du produit scalaire. Déduiser en l'expression de r en fonction du temps.
  4. On appelle a l'angle de OM et V. Calculer en fonction de a, le module du vecteur accélération de M et le rayon de la courbure de la trajectoire de M.
corrigé

D'après la définition de l'accélération, celle ci est perpendiculaire au plan défini par le vecteur vitesse et le vecteur position. Donc l'accélération tangentielle, colinéaire au vecteur vitesse est nulle.

Intégrer et déterminer la constante en écrivant qu'à t=0 le produit scalaire est nul (vecteurs vitesse initiale et position perpendiculaires)

Intégrer et déterminer la constante en écrivant qu'à t=0 le rayon r est égal à d.

r²= v0²t² + d²

à partir du produit scalaire :

r²cos² a = v0² t²

r²-r²cos² a = r²sin²a = r²-v0² t²= d²

d'où : r sina = d

à partir du produit vectoriel :

rayon de courbure :

l'accélération tangentielle étant nulle G= gN= v0²/r.

retour - menu