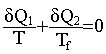Aurélie fevrier 2001

pompe à chaleur réversible fonctionnant avec 2 sources

Google

1

travail

entropie

performance

Une pompe à chaleur réversible échange de la chaleur avec 2 sources, l'eau d'un lac (Tf=280K) , et une réserve d'eau de masse M=1000 kg isolée thermiquement ; la température initiale de cette dernière est T0=293K. ceau = 4190 J K-1 kg-1. Lorsque la masse d'eau M atteint la température de T=333 K, calculer :

  1. Les transferts thermiques pompe réserve et pompe eau du lac.
  2. Le travail reçu par la pompe.
  3. La variation d'entropie de la source froide.
  4. Le coefficient moyen de performance de la pompe à chaleur.
corrigé

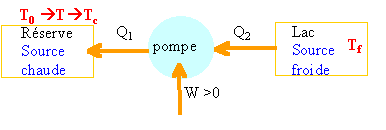
lors d'un cycle et un fonctionnement réversible:

premier principe : dQ1+dQ2+dW=0

second principe :

avec dQ1 = - mc dT ce qui part de la pompe est négatif.

transfert thermique cédé par l'eau du lac :

-m c / T dT = dQ2 /Tf

Q2 = Tf m c ln (Tc / T0)

Q2 = 280*4190*1000 ln (333 / 293) = 150 MJ.

transfert thermique reçu par l'eau de la réserve :

Q1 = - M c (Tc-T0) = -1000*4190*(333-293) = - 167,6 MJ.

travail reçu par la pompe :

W+Q1+Q2 =0

W= 167,6-150 =17,6 MJ.

variation d'entropie

de la source froide qui reste à température constante Tf : -Q2 / Tf

-1,5 108 / 280 = -5,357 105 J K-1.

coefficient moyen de performance de la pompe :

rapport de la chaleur absorbée par la source chaude sur le travail fourni

|Q1| / W = 167,6 / 17,6 = 9,52.

Pompe à chaleur réversible :

Une pompe à chaleur réversible fonctionne entre un lac dont la température est constante et vaut q0=10°C et une masse M d'eau thermiquement isolée, à la température initiale q1=20°C . Cette masse d'eau est chauffée.

  1. Quelle relation existe-t-il entre la température de l'eau T et le travail W fourni par la pompe ?
  2. Calculer W pour M=1 tonne quand la température finale de l'eau est q = 50°C.
  3. Quelle aurait été l'élévation de température si la même énergie W avait été fournie par une résistance chauffante ? ceau = c = 4,18 kJ K-1 kg-1.
corrigé
La pompe à chaleur fonctionne selon un cycle réversible de Carnot ; son efficacité e vaut :

e= d Q1/dW = T/(T-T0)

avec T : température de la source chaude et T0, température de l'eau du lac

dQ1, transfert thermique reçu de la part de l'eau du lac ( source froide) : d Q1=Mc dT.

travail d W fourni par le moteur de la pompe : d Q1(T-T0)/ T = d Q1(1-T0/ T)

d W = Mc (1-T0/ T) dT

intégration : W= Mc[T1-T0)-T0ln(T1/T0)]

T1= 273+50 =323 K ; T0= 283 K

W=1000*4,18[323-283-283 ln(323/283)]=10 809 kJ.

En fournissant cette énergie à une résistance chauffante, l'élévation de température aurait été de :

W= Qjoule= McDT soit DT = Qjoule/( Mc)=10809/4180=2,6°C.

retour - menu

à suivre