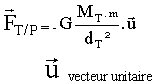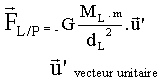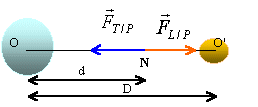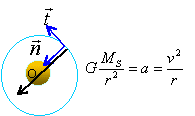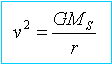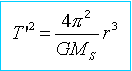Aurélie sept 2000

devoirs en terminale S

A propos de quelques satellites d'observation

Google

1

Terre - Lune

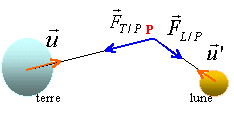
Jules Verne, dans " De la Terre à la Lune " (1865), fait allusion au " point neutre N ", situé à 350 000 km du centre de la Terre, où les forces gravitationnelles exercées par la Terre et la Lune sur un obus se compensent.

Le satellite SoHO (Solar and Heliospheric Observatory) fait partie d'un vaste programme international de recherche sur les relations Terre-Soleil...... et met en oeuvre plusieurs satellites, de nombreux télescopes, radars et instruments divers. Construit par l'ESA (Agence Spatiale Européenne) sous maîtrise d'oeuvre Matra-Marconi Space, il a été lancé, en décembre 1995, par une fusée américaine Atlas en direction du " point de Lagrange 1 ", une zone située à 1,5 million de kilomètres du centre de la Terre, où les forces d'attraction de notre globe et celles du Soleil s'équilibrent.

On considère que la Terre, la Lune et le Soleil sont des corps à répartition sphérique de masse.

  • Distance moyenne Terre - Lune ou rayon de l'orbite lunaire : D= 3,8 5 108 m
  • Distance moyenne Terre-Soleil ou rayon de l'orbite terrestre : D=1,5 5 1011 m
  • Période de révolution de la Terre autour du Soleil : T =365 jours
  • On appelle MT , ML et MS les masses respectives de la Terre, de la Lune et du Soleil et on considère que MT =(9)². ML ; MS =(580)² . MT
  • Constante de gravitation : G = 6,7 5 10-11 N.m².kg-2
  1. Donner l'expression vectorielle de la force gravitationnelle exercée par la Terre sur un objet ponctuel P de masse m situé à la distance dT du centre de la Terre et celle de la force gravitationnelle exercée par la Lune sur ce même objet P, dL étant la distance de P au centre de la Lune.
  2. Montrer que le " point neutre N " auquel fait allusion Jules Verne est nécessairement situé, d'une part sur la droite joignant le centre de la Terre et le centre de la Lune et, d'autre part entre ces deux points.
  3. Montrer que la distance d ( distance du centre de la Terre au " point neutre N ") est égale aux neuf dixièmes de la distance Terre - Lune et retrouver ainsi la valeur annoncée par Jules Verne.

     

corrigé

D'après la loi de gravitation (Loi de Newton), la force gravitationnelle exercée par la Terre (corps supposé être à répartion sphérique de masse) sur l'objet ponctuel P est égale à :

Pour la force gravitationnelle exercée par la Lune (corps supposé être à répartion sphérique de masse) sur l'objet :

D'après la définition du point neutre les deux forces gravitationnelles exercées sur l'objet, doivent être opposées, (même direction, même valeur et sens contraire).

Les trois points O, O', N doivent être alignés, et N doit être entre O et O'.

D-d voisin de D donc d voisin de 9 D

Le point neutre est environ au 9/10 de la distance terre lune , à partir de la terre.
2

Soleil - Terre
  1. On peut définir aussi un " point neutre N' " dans le cas de la Terre et du Soleil. En faisant un raisonnement analogue, on peut évaluer l'ordre de grandeur de la distance d' (distance du centre de la Terre au point neutre N') dans le cas Terre- Soleil ; d' est-elle de l'ordre de :

    8,7 1013 m 1,5 109 m 2,6 108 m ?

  2. En comparant d' avec la position du " point de Lagrange 1 ", peut-on considérer que celui-ci est un point neutre ?
corrigé

 

même raisonnement que ci dessus le soleil jouant le rôle de la terre et la terre celui de la lune.

le point cherché est plus proche de la masse la plus petite , soit plus proche de la terre

MS = (580)².MT donc (D-d )*580 = d avec d voisin de D

D-d voisin de 2,6 108 m

c'est à dire dix fois plus petit que la distance donnée dans le texte pour le point de Lagrange 1
3

satellite du soleil

Considérons maintenant un satellite de masse m. Il évolue sur une orbite circulaire de centre O, centre du Soleil, de rayon r. On veut étudier le mouvement de ce satellite.

  1. Dans quel référentiel faut-il faire l'étude ?
  2. Montrer que, si ce satellite n'est soumis qu'à la force gravitationnelle exercée par le Soleil, alors son mouvement circulaire est uniforme. Établir l'expression de la valeur v de sa vitesse.
  3. Établir l'expression de sa période en fonction de G, Ms et r
  4. SoHO est un satellite du Soleil tel qu'à chaque instant, le centre du Soleil, SoHO (assimilé à un point) et le centre de la Terre sont alignés. Quelle est la période de SoHO ?
  5. Peut-on dire que SoHO placé au point de Lagrange 1 n'est soumis qu'à la force gravitationnelle exercée par le Soleil ? Justifier clairement la réponse.
corrigé

étude dans le référentiel héliocentrique.

On étudie le mouvement du satellite (point matériel) dans ce référentiel, galiléen. Le vecteur accélération vérifie le théorème du centre d'inertie :

La seule force appliquée est la force gravitationnelle exercée par le soleil.

le vecteur accélération est dirigé vers le centre du soleil.

La composante de l'accélération étant nulle suivant le vecteur t de la base de Frenet, la norme du vecteur vitesse ne change pas (mouvement uniforme)

La période de révolution T' du satellite est le temps mis par le satellite pour faire un tour et ce d'un mouvement uniforme.

2 p r =vT'

hypothèse, centres du soleil de la terre et SoHO alignés :

la période de SoHO est égale à la période de révolution de la Terre autour du Soleil soit environ 365 jours.

la période de révolution T' d'un satellite soumis à la seule force gravitationnelle exercée par le Soleil ne dépend que du rayon r de l'orbite ( T² = K . r3 ).

Le rayon de la trajectoire de SoHO devrait être égal à celui de l'orbite de la Terre ; ce n'est pas le cas, donc il y a au moins une autre force à considérer. 

retour - menu

à suivre