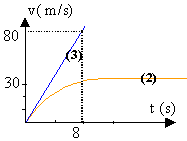Aurélie mai 2001


devoirs en terminale S

étude de la chute d'une goutte d'eau Polynésie 09 /98

Google


 

1

 

 

chute

poussée d'Archimède

frottement vitesse limite

Données :

volume d'une sphère : 4/3 p R3.

masse volumique : eau 1000 kg/m3; air 1,3 kg/m3.

g= 9,8 m/s² ; coefficient de viscosité de l'air : h =1,81 10-5 kg s-1 m-1.

coefficient de frottement fluide d'une sphère de rayon R se déplaçant dans l'air : f= 6phR.

rayon de la goutte étudiée : R= 0,5 mm

volume de la goutte : V=5,2 10-10 m3.

masse de la goutte : m = 5,2 10-7 kg

cofficient de frottement fluide : f= 1,7 10-7 kg s-1.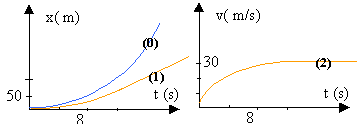

Chute libre de la goutte :

La goutte d'eau est supposée tombée dans le vide, sans vitesse initiale, à partir d'un point O choisi comme origine d'un axe Ox vertical vers le bas.

  1. établir les équations horaires de sa vitesse v(t) et de sa trajectoire x(t)
  2. Tracer la courbe v(t) sur le graphe (2). La courbe x(t) correspond à la courbe (0).
    Pour réaliser une étude plus réaliste de la chute de la goutte dans l'air, il faut tenir compte d'autres forces

la Poussée d'Archimède :

  1. "Tout corps plongé dans un fluide subit une poussée verticale dirigée de bas en haut, égale au poids du fluide déplacé". Quels sont le volume, la masse du volume d'air déplacé par la goutte, puis le poids du volume d'air déplacé.
  2. Comparer au poids de la goutte d'eau et conclure.

force de frottement:

  1. La force de frottement est un vecteur colinéaire au vecteur vitesse, de sens contraire , de norme f v. Calculer la valeur de cette force si la vitesse vaut 10 m/s.
  2. Comparer cette force au poids et conclure.

équation différentielle du mouvement de la goutte:

  1. Réaliser l'inventaire des forces qui s'exercent sur la goutte en mouvement et les représenter sur un schéma.
  2. La vitesse vérifie l'équation différentielle :v' + f/m v = g . Quelle est la loi qui conduit à cette relation? Commenter la signification physique des termes qui y figurent.
  3. La solution de l'équation différentielle précédente est représentée par la courbe (2). On peut par intégration déterminer l'équation horaire du mouvement x(t) qui est représentée par la courbe (1). Evaluer l'ordre de grandeur de la distance au delà de laquelle les frottements se font dentir de façon sensible.
  4. Que devient la nature du mouvement au bout d'une dizaine de secondes?

vitesse limite:

  1. Déterminer d'après les courbes la vitesse limite de la goutte.
  2. En exploitant l'équation différentielle, déterminer l'expression de la vitesse limite; la calculer et la comparer à la valeur précédente.

influence de la taille de la goutte:

  1. On suppose que le rayon de la goutte est 2 fois plus grand R= 1 mm. Etudier l'influence de cette modification sur la vitesse limite de la goutte. Conclure.

corrigé


accélération g; vitesse initiale 0; position initiale 0.

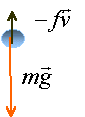v(t) primitive de l'accélération: v(t) = gt

x(t) primitive de la vitesse : x(t) = ½ gt²

poussée : rair g V avec rair = 1,3 kg/m3.

poids : reau g V avec reau = 1000 kg/m3.

reau >>rair donc la poussée est négligeable devant le poids.

frottement : F= f * v = 1,7 10-7 *10 = 1,7 10-6 N

poids : 5,2 10-7 * 9,8 = 5,1 10-6 N

poids et frottements sont du même ordre de grandeur.

La deuxième loi de Newton , projetée sur un axe vertical orienté vers le bas s'écrit : mx" = mg -fv

soit x" +f/m v = g ou v' + f/ m =g

le premier terme est l'accélération de la goutte;

le second est la décélération due au frottement;

le troisième est l'accélération de la pesanteur (chute libre)

au dela de quelques dizaines de mètres de chute (courbe (1)), il faut tenir compte des frottements.

au dela de 10s, la vitesse limite est atteinte ( voisine de 30 m/s); l'accélération est nulle et le mouvement est rectiligne uniforme.

L'accélération étant nulle lorsque la vitesse limite Vl est atteinte, l'équation différentielle s'écrit :

0 +f/m Vl = g d'où Vl = mg/ f = 5,2 10-7*9,8 / 1,7 10-7 = 30 m/s.

Le coefficient f est proportionel au rayon de la goutte.

si la masse m de la goutte ne change pas, alors la vitesse limite de la goutte est deux fois plus petite

si la masse de la goutte change: la masse est proportionnelle au volume donc au rayon au cube, alors la vitesse limite est proportionnelle à R² et la vitesse limite quadruple.


à suivre ...
retour - menu
à bientôt ...