| |
le lancer du poids Antilles 09 /98
|
||||||
|
|
résistance de l'air trajectoire énergie |
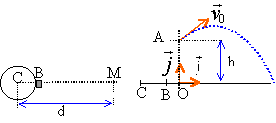
En 1990 ,'américain Randy Barnes établit le record du mondede lancer du poids : la distance atteinte est d= 23,12 m. Le poids est constitué par une sphère homogène métallique lisse de masse m= 7,26 kg. L'aire de lancement est constituée d'un cercle métallique de diamètre D= 2,14 m et par un butoir B. La portée du jet est mesurée à partir du centre C du cercle. A l'issue de la phase d'élan le pois est abandonné en A, à la hauteur h= 2m au dessus du sol horizontal, à la distance BO= 0,35 m en avant du butoir B. Le bras qui lance fait alors un angle de 45° avec l'horizontale. Cet angle est celui de la direction du vecteur vitesse initiale v0 avec l'horizontale. Choix d'un modèle : La résultante des forces de frottements dues à l'air est donnée par : R= ½ r Cx S V² où r est la masse volumique de l'air 1,9 10-3 kg /m3, S l'aire de la section équatoriale de la sphère 1,13 10-2 m², Cx un coefficient caractéristique de la forme de l'objet Cx = 0,5 S.I et V la valeur de la vitesse.
Etude du mouvement :
aspect énergétique:
|
|||||
| |
masse volumique r :[kg] [m]-3. surface S : [m]² vitesse au carré : V² en [m]² [s]-2. soit rSV² en [kg] [m][s]-2. donc Cx sans dimension. R= 0,5 *1,29 * 0,5 *1,13 10-2 *100 = 0,364 N poids : mg = 7,26*9,1 = 71,2N très supérieur (200 fois) à R. vitesse initiale : [V0 cos 45 ; V0 sin 45 ] accélération de la pesanteur : [ 0, -g] position initiale [0 ; 2 ] vitesse à une date t : [V0 cos 45 ; -gt +V0 sin 45] position à une date t : x = V0 cos 45 t ; y = -½ gt² +V0 sin 45t + h trajectoire : y = - ½ gx² / (V0 cos 45)² + x tan 45 + h y = -9,8 x² / V0² + x + 2 le mouvement est rectiligne uniforme sur l'axe des abscisses. le mouvement est uniformèment accéléré sur l'axe des ordonnées. au point d'impact sur le sol : x = 23,12 - 1,07 - 0,35 = 21,7 m 0 = -9,81 *21,7² / V0² +21,7 +2 d'où V0 = 13,95 m/s. durée du déplacement AM : xM= 21,7 m soit 21,7 = 14 * cos 45 t d'où t = 2,19 s. vitesse au point d'impact : Vx = 14*cos45 = 9,9 ; Vy = -9,8*2,19 + 14*sin 45 = -11,58 V² = 9,9 ² + (-11,58)² = 232,19 d'où VM = 15,23 m/s. énergie cinétique initiale : ½mV0² = 0,5*7,26 *14² = 711,4 J énergie potentielle initiale : mgh = 7,26*9,8*2 = 142,4 J énergie mécanique initiale : ½ mV0² + mgh énergie mécanique finale (point d'impact) :½ mVM² conservation de l'énergie mécanique : ½ mV0² + mgh = ½ mVM² VM² = V0² + 2gh = 14² +2*9,8*2 = 235,2 d'où VM= 15,33 m/s. résultat cohérent avec celui trouvé ci dessus.
|
||||||
|
|
|