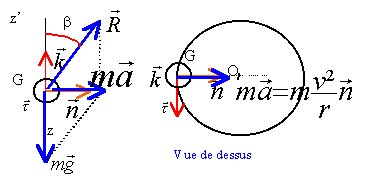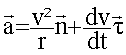| |
TGV et train pendulaire Liban 06/99
|
||||||
|
|
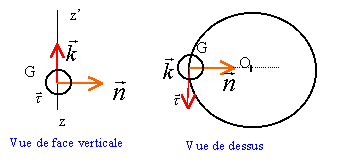
repère de Frenet Mvt circulaire virage incliné |
Le TGV nécessite une infrastructure particulière avec des virages de très grand rayon de courbure car le rail extérieur ne peut être que faiblement relevé (inclinaison b du plan des rails par rapport à l'horizontale). Une alternative moins couteuse est obtenue avec le train pendulaire qui utilise le réseau normal et permet de passer plus vite les virages qu'untrain classique et dans de meilleurs conditions de confort pour les passagers, surtout en région montagneuse où les rayons de courbure sont faibles. Le plancher de la caisse d'un TGV reste pratiquement parallèle au plan des rails et son inclinaison par rapport au plan horizontal reste égale à l'angle b alors que la caisse d'un train pendulaire est articulée et permet une inclinaison supplémentaire q de son plancher par rapport au plan des rails. Le confort des passagers est optimal lorsque l'action des rails sur le wagon assimilée à une force unique R est perpendiculaire au plancher de ce wagon. On se propose de comparer le comportement en virage pour les 2 trains de même masse m, en étudiant le mouvement dans un plan horizontal, de leur centre d'inertie G, lors d'un virage de rayon r, pris à la vitesse de valeur constante v. g=9,8 ms-2. 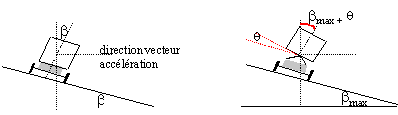 étude préliminaire :
applications :
|
|||||
| |
tan b = ma / mg avec ma =mv²/r d'où tan b = a / g = v² /(rg) cos b = mg / R d'où R = mg / cos b. ou bien sin b = ma / R d'où R = ma / sin b = mv² / (r sin b). vitesse en m/s : 320 / 3,6 = 88,9 m/s rayon en m : 9000 m tan b = 88,9² / (9000*9,8 ) =0,089 et b = 5,1° R = 40 000*9,8 / cos 5,1 = 3,93 105 N vitesse maxi du train pendulaire : bmax+q = 12° et r = 1000 m v2² = tan 12 * 1000*9,8 = 2,08 103. d'où v2 = 45,64 m/s ou 45,64*3,6 = 164,3 km/h gain relatif : 134 / 3,6 = 37,22 m/s. 100* (45,64-37,22) / 37,22 = 22,6%.
|
||||||
|
|
|