Aurélie mai 2001


devoirs en terminale S

lecteur de compact disque sujet complémentaire

Google


 

1

 

longueur d'onde

indice

interférences

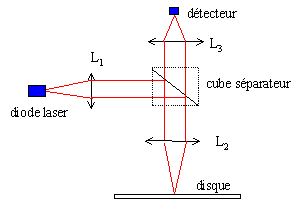
La lumière émise par une diode laser est transformée en une onde plane gràce à la lentille L1. Le faisceau de lumière parallèle est partiellement réfléchi (50%) par le cube séparateur. La lentille L2 permet de focaliser le faisceau sur le disque optique. La lumière réfléchie repasse par L2, traverse le cube séparateur pour être focaliser par la lentille L3 sur le détecteur.

Le disque est composé d'une surface réfléchissante sur laquelle sont aménagées des cavités de matériau transparent homogène d'épaisseur e et d'indice de réfraction n.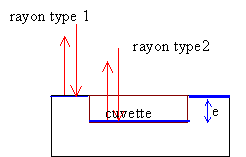 

  1. On suppose que le faisceau de lecture éclaire le bord d'une cuvette de sorte que l'énergie lumineuse se répartit de façon symétrique sur la surface du disque et sur le fond de la cuvette .Deux types de rayons se propagent : ceux de type 1 qui sont réfléchis à la surface du disque et ceux de type 2 qui sont réfléchis au fond de la cuvette. Les deux rayons sont supposés perpendiculaires aux surfaces Déterminer la différence des distances parcourues par les rayons de type 1 et 2 ,en supposant les trajets dans l'air identiques .Soit d cette différence.Ecrire la condition d'interférence constructive .
  2. La source laser est monochromatique de longueur d'onde l0. Quelle est la longueur d'onde l de ce rayonnement dans le matériau d'indice n .Ecrire la condition d'interférence constructive en fonction de l ,puis de l0.On appelle chemin optique la grandeur d=nd. Ecrire la condition d'interférence constructive en faisant intervenir d et l0 .Ecrire la condition d'interférence destructive en faisant intervenir d et l0 .Quelle est la plus petite épaisseur e qui puisse donner cette interférence ;exprimer e en fonction de n et l0 .Application numérique n=1,5 ; l0 =680 nm .
  3. Que se passe t-il si le faisceau est totalement réfléchi par la surface du disque ou totalement réfléchi par le fond d'une cuvette.
  4. Le faisceau de lecture est caractérisé par son diamètre e' au niveau du disque. Evaluer la plus petite surface s que doit avoir une cuvette .En supposant que le nombre N d'informations enregistrables sur le disque optique est le rapport entre la surface enregistrable et la surface s d'une cuvette ,déterminer N.

R1=2,2 cm ; R2 = 5,8 cm ; e' = 2,7 mm.

corrigé



 

la différence des distance parcourues par les rayons de type 1 et de type 2 (en supposant les trajets dans l'air ) est égale à 2 fois l'épaisseur de la cuvette soit 2e.

Les interférences sont constructives si la différence des trajets ( supposés dans l'air ) est un multiple de la longueur d'onde l0 dans l'air.

la fréquence caractérise une onde.

alors que vitesse de propagation et longueur d'onde dépendent du milieu de propagation.

l0 = c / fréquence = 3 108 / f

l = v / fréquence d'où l0 / l = c / v

or c / v = n indice de réfraction du milieu ( nombre positif supérieur à 1)

l0 / l = n

interférences constructives:

différence des distances = k l0= k n l .( k appartient à Z)

chemin optique : d = nd = 2 n e = k l0

interférences destructives

la diférence de chemin optique est égal à un multiple impair de demi longueur d'onde

d = (2k+1) l0 / 2 = 2ne

la plus petite épaisseur correspond à k=0 soit : e = l0 / (4 n)

e = 680 / (4*1,5 ) = 680 / 6 = 113 nm.

si le faisceau est totalement réfléchi par la surface du disque, la différence de chemin optique est nulle : les interférences sont constructives.

Même chose si le rayon est totalement réfléchi par le fond d'une cuvette.

cuvette circulaire de rayon e' = 2,7 10-6 m

surface s = p e'² = 3,14 * (2,7 10-6)² =2,289 10-11 m².

surface d'enregistrement : p (R2²-R1²)

3,14 (5,8²-2,2²) 10-4 =9,0432 10-3 m²

nombre d'informations N = 9,0432 10-3 / 2,289 10-11 = 3,9 108.

 


à suivre ...
retour - menu
à bientôt ...