Aurélie avril 2001


devoirs en terminale S

oscillateur : équation horaire, énergies.

 

Google



1

représentations graphiques

On suppose que les frottements sont négligeables. Un pendule simple est écarté de sa position d'équilibre d'un angle a=30° puis abandonné sans vitesse initiale.L'objet suspendu de masse m=200g est assimilable à un objet ponctuel. La longueur du fil est L =0,8m et g=9,8m.s-2. On repère la position du pendule à l'instant t par l'angle a du pendule avec sa position d'équilibre.On considère que le pendule, dans les conditions de l'expérience, peut être assimilé à un oscillateur harmonique de période propre T=2p racine carrée(L/g).

  1. Détreminer l'équation horaire a =f(t) du mouvement du pendule et l'expression de a '=h(t) de sa vitesse angulaire. Conditions initiales:t=0, a=30°,V=0.
  2. Tracer dans un même repère a et a '(avec des échelles différentes).
  3. En déduire les expressions de Ec et Ep en fonction de t.
  4. Tracer dans un même repère Ec et Ep. Quelle est la période de Ep et Ec ?

corrigé


 

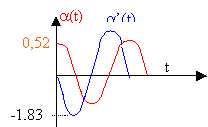
exprimer les angles en radians: 30°= p/6 = 3,14/6 = 0,523 rad

a(t) = 0,523 cos (wt+ j)

w = 2 p fréquence

période = 6,28 racine carrée (0,8/9,8)=1,8 s et f= 0,557 Hz et w= 3,5 rad /s

a(t) = 0,523 cos(3,5 t + j)

à t=0 alors a=30° = 0,523 rad

0,523 = 0,523 cos (0+j) d'où j =0.

a(t) = 0,523 cos(3,5 t ).

vitesse angulaire = a'(t)=0,523*3,5 (-1) sin (3,5t) =-1,83 sin(3,5t)

a'(t) = -1,83 sin(3,5t).

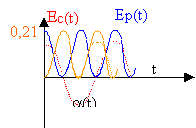
énergie cinétique : 0,5 mv² avec v = a'L =0,8 *a' et m= 0,2 kg

Ec = ½*0,2 *0,8² (-1,83 sin(3,5t))² = 0,214 sin²(3,5t) joules

la période de la fonction sin² x est la moitié de la période de la fonction sin x

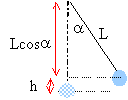
Energie potentielle (origine : position d'équilibre) mg h

avec h = L(1-cos a).

Ep= 0,2*0,8*9,8(1-cos a )

ou bien écrire que l'énergie mécanique se conserve:

au départ l'énergie mécanique est sous énergie potentielle de pesanteur :

0,2*0,8*9,8(1-cos 30 ) =0,214 J

à la date t : Ep= 0,21 -Ec=0,214(1 -sin²(3,5t))

à t=0 toute l'énergie est sous forme potentielle.

à t= 0,45 s ( 0,25 période) toute l'énergie est sous forme cinétique.

à t=0,9 s toute l'énergie est sous forme potentielle.

à t= 1,35 s ( 0,75 période) toute l'énergie est sous forme cinétique.


à suivre ...
retour - menu
à bientôt ...