| |
lâcher d'une balle et rebond.
|
||||||
|
|
trajectoire énergie cinétique hauteur maxi
|
Un enfant lâche une balle de tennis (m=57g), sans vitesse initiale, d'une hauteur de 6 m au dessus d'une verrière oblique. La balle rebondit en A sur la verrière, symétriquement par rapport à la normale à la verrière et sans changement de la valeur de la vitesse. Elle atteint le sol en B. 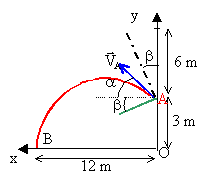
rappel : 1+ tan² a = 1 / cos² a.
|
|||||
| |
l'énergie potentielle (origine au sol) de pesanteur initiale est convertie en énergie cinétique énergie cinétique en A égale diminution de l'énergie potentielle de pesanteur 0,5 mv²= mgh =0,057*9,81*6= 3,355 J. d'où la vitesse en A : rac carrée(3,355 *2/0,057)=117,6 VA = 10,84 m/s. énergie cinétique au sol = énergie
potentielle initiale = 0,057*9,81*9 = 5 J.
axe vertical (y) vers le haut axe horizontal (x) à gauche au départ : vitesse (VA cos a ; VA sin a ) accélération (0, -9,81) position initiale (0 ; 3) à la date t : vitesse (VA cos a ; -9,81 t +VA sin a) position : x = VA cos a t ; y = -4,9 t² +VA sin a t +3 parabole : y= -4,9 x² / (VA²
cos² a ) + x tan a +3
0 = -4,9 *12*12/(117,6 cos² a ) +12 tan a +3 0 = -6 / cos² a +12 tan a +3 0= -6(1+tan² a ) +12 tan a +3 résoudre l'équation du second degré en posant X = tan a X= 0,293 et angle = 59,63° X= 1,707 et angle =16,33° angle de la verrière par rapport au sol : b = (90 - a ) / 2 deux valeurs : 15,3° et 36,8 °.
la composante verticale de la vitesse nulle -9,8t +VA cos a =0 t = VA cos a / 9,8 repport dans y y maxi = 1/ (2*9,8)*(VA² sin ² a ) +3 remplacer a par ses valeurs 16,33 puis 59,63 °. 3,47 m et 7,46 m
|
||||||
|
|
|