| |
oscillateur en régime forcé Asie juin 2000
|
||||||
|
|
oscillateur élastique résonance impédance du circuit RLC |
oscillateur élastique vertical : détermination de sa fréquence propre. L'oscillateur est constitué d'un ressort vertical de masse négligeable, de constante de raideur k, de longueur à vide 0,1 m auquel est suspendu un solide de masse 50 g.
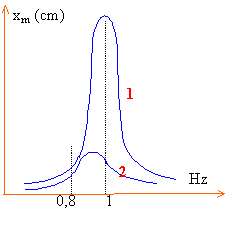
oscillateur élastique soumis à une excitation sinusoïdale. 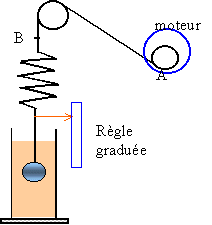 La vitesse de rotation du moteur est réglable. Larbre est muni d'un exentrique A. Le point A décrit un cercle de rayon A. Le point B est animé d'un mouvement sinusoïdal d'amplitude a. La fréquence du point B est proportionnelle à la vitesse angulaire du moteur. Le moteur constitue l'excitateur et le pendule vertical est le résonateur. Moteur arrèté, on détermine la fréquence propre du résonateur élastique non amorti en mesurant 10 périodes. On trouve f0 = 1Hz. L'éprouvette contenant de l'eau a été retirée pour cette mesure. Moteur lancé: l'amplitude xm des oscillations du résonateur dépend de la fréquence de l'excitateur. On effectue deux séries de mesures: cas 1 , cylindre non immergé et cas 2, cylindre immergé.
On considère l'association série, conducteur ohmique R2=400W, bobine L=0,1H, R=50W et condensateur C=0,1 mF. Aux bornes du dipôle on place un GBF qui impose une tension sinusoïdale telle que : u(t) =Um sin (2pft) = Um sin (wt). On dispose d'un oscilloscope bicourbe et de 2 multimètres à affichage numérique.
|
|||||
| |
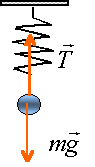
A l'équilibre le poids est opposé à la tension et la tension est proportionnelle à l'allongement du ressort. mg=k(L-L0) masse en kg; L-L0 en mètre k = 0,05*9,8 / (0,12-0,1)= 24,5 Nm-1. oscillations libres non amorties (pas de frottements) période : T=2p racine carrée (m/k) T=2*3,14 racine carrée (0,05/24,5) =0,2837 s fréquence = 1 / 0,2837 =3,52 Hz.
cas 1 : oscillations forcées avec un amortissement faible la résonance est aigue, pic étroit f0 = 1 Hz cas 2 : oscillations forcées avec un amortissement important résonance floue, abscence de pic aigu. f0 = 0,9 Hz 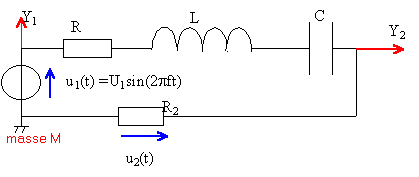
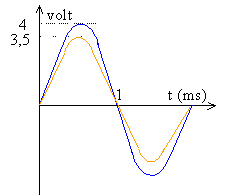
La tension aux bornes du résistor R2 est proportionnelle à l'intensité. Observer la tension aux bornes de R2, c'est observer l'image de l'intensité au facteur R2 près. A la résonance d'intensité, la tension aux bornes du dipole et l'intensité qui le traverse sont en phase. La période est voisine de 2 ms et la fréquence voisine de 1/ 0,002 = 500 Hz. Um = 4 volts et R2Im = 400 Im =3,5 volts Im = 3,5 / 400 = 8,75 mA. impédance Z = Um / Im = 3,5 /0,00875 = 400 W. A la résonance d'intensité, l'impédance du dipole RLC est minimale, égale à la somme des résistance du circuit soit 400+50 =450 W.
|
||||||
|
|
|