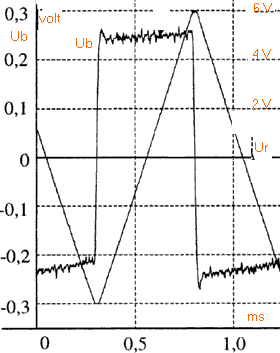
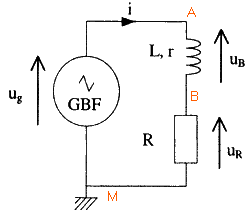
On dispose :

- d’un générateur basse fréquence (GBF) dont une des bornes de sortie est reliée à la masse. Il délivre une tension alternative symétrique triangulaire d’amplitude U=6V et de fréquence f réglable ;

- d’une bobine d’inductance L = 0,1 H et de résistance r =10 W.;

- d’un conducteur ohmique de résistance R=10 kW .

On réalise le montage de la figure ci-dessous.

1. Ajouter au schéma les branchements à effectuer pour visualiser les tensions u_g sur la voie 1 et u_R sur la voie 2 d’un oscilloscope.
2. L’une de ces tensions permet d’observer l’allure de l’intensité i du courant. Laquelle ? Justifier la réponse.
3. On considère le schéma du montage ci-dessus.
   * Exprimer u_B en fonction de u_g et de u_R
   * Exprimer la tension u_B aux bornes de la bobine en fonction de r, i et de la f.é.m d’auto-induction e dans la bobine, en respectant l’orientation choisie, puis en fonction de r, L, i , di / dt.
4. La courbe ci-dessus donne l’allure des tensions u_B et u_R : il est obtenu par saisie automatique puis traitement informatique des tensions u_g et u_R.

• Déterminer la période T de l’intensité du courant.
• Déterminer l’amplitude (valeur maximale atteinte) de l’intensité du courant.
• On considère sur ces courbes, une demi-période où la tension u_B est positive. Déterminer une valeur approchée de la tension u_B en admettant qu’elle est constante.
• Montrer que la dérivée par rapport au temps de l’intensité du courant vaut : di / dt =2,4 As^-1.
• En déduire l’ordre de grandeur de la valeur L de l’inductance de la bobine en négligeant l’influence de la résistance r.
• La résistance r de la bobine étant égale à 10W, comparer rI_max et |e| et en déduire si l’hypothèse "négliger l'influence de r " était justifiée.

  ---

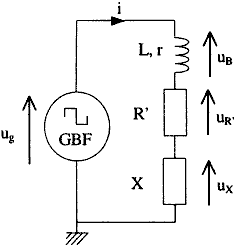
On réalise un nouveau montage (figure ci-dessous) en plaçant en série :

- le GBF (dont une des bornes de sortie est reliée à la masse) qui délivre maintenant une tension alternative symétrique, en créneaux ;

- la bobine utilisée dans la question 1 ;

- un conducteur ohmique de résistance R'=500W;

- un dipôle X.

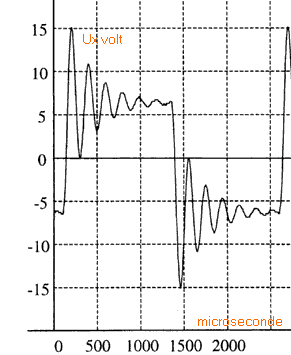
On visualise la tension aux bornes de ce dipôle. On obtient la courbe ci dessus.

• Comment appelle-t-on le phénomène visualisé sur cette courbe ?
• Identifier le dipôle X parmi les dipôles suivants : conducteur ohmique, bobine, condensateur.
• Donner l’ordre de grandeur de la pseudo-période.
• En déduire une valeur approchée de la grandeur caractéristique du dipôle X en assimilant la pseudo-période à la période propre (période lorsque l’influence des résistances est négligeable).