Aurélie janvier 2001


devoirs en terminale S

oscillateur élastique mécanique (Pondichéry bac avril 96)

Google


 

1

raideur

période

énergie

 
  1. Dans tout l'exercice, on prendra g = 10 m / s2. On négligera les frottements. On utilise un ressort de masse négligeable, à spires non jointives.
    1. Etude préalable du ressort

    Pour déterminer la raideur k d'un ressort, on accroche une de ses extrémités à un support fixe. Lorsqu'on accroche une masse marquée m = 200 g à son autre extrémité, son allongement vaut 10,0 cm.

  2. Vérifier que la raideur du ressort vaut 20,0 N.m - 1.
  3. En utilisant le théorème du centre d'inertie, justifier que la raideur peut aussi s'exprimer en kg/s2.
  4. En quelle unité la quantité racine carrée (m /k )s'exprime-t-elle ?

    2. Etude d'un oscillateur élastique

  5. On fixe maintenant le ressort étudié comme l'indique la figure ci dessous. Le ressort est horizontal ; une de ses extrémités est fixe. On accroche à son autre extrémité un solide (S) masse m = 200 g. Ce solide peut se déplacer sans frottement le long d'un axe horizontal Ox. À l'équilibre, le centre G du solide coïncide avec l'origine 0 du repère. Etablir l'équation différentielle qui régit le mouvement de G.
  1. En déduire l'expression de la pulsation propre w0 de cet oscillateur et celle de sa période propre T0. Calculer numériquement w0 et T0.
  2. Vérifier que, quelles que soient les valeurs de Xm et j, l'équation horaire x (t) = Xm cos (w0 t + j) est solution de l'équation différentielle précédente.
  3. On comprime le ressort vers la gauche. Le point G occupe alors la position Go telle que OGo = - 0,15 m. À l'instant t = 0, on lâche le solide sans vitesse initiale. Déterminer l'amplitude Xm et la phase j du mouvement, ainsi que l'expression de la vitesse v (t) du solide. En déduire la valeur maximale de la vitesse.
  4. Définir et exprimer l'énergie mécanique de cet oscillateur non amorti. Calculer sa valeur à l'instant t = 0. (On prendra l'énergie potentielle du ressort nulle lorsque x = 0).
  5. En admettant et en utilisant la conservation de cette énergie mécanique, retrouver la valeur maximale de la vitesse du solide.

     

corrigé



 

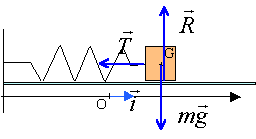
A l'équilibre du ressort vertical, le poids est opposé à la tension ; la tension et l'allongement sont proportionnels.

mg = k x

m = 0,2 kg ; g = 10 m/s² ; x = 0,1 m d'où k =0,2*10 / 0,1 = 20 Nm-1.

une force est équivalente au produit de la masse par une accélération.

[N] équivalent à [kg][m][s]-2.

raideur [N] [m]-1équivalent à [kg][s]-2.

masse divisée par raideur :[kg] / [kg][s]-2) équivalent à [s]2.

et racine carrée (m / k ) homogène à une durée en seconde.

écrire la 2 ème loi de Newton sur l'axe horizontal :

-kx = m x" soit x"+ k/m x=0 ou encore x" +w0² x=0 (1)

avec w0² =k / m =20 / 0,2 =100

w0 = 10 radians / s et T0 = 2p / w0 = 6,28 /10 =0,628 s

x (t) = Xm cos (w0 t + j)

dériver par rapport au temps pour avoir la vitesse

x' = -Xm w0sin (w0 t + j) (2)

dériver la vitesse par rapport au temps pour avoir l'accélération

x" = -Xm w0²cos (w0 t + j) = -w0²x

repport dans l'équation différentielle (1)

-w0²x +w0²x = 0 vrai pour tout x

amplitude (toujours positive Xm ) = 0,15 m

x (t=0) = 0,15 cos ( j) = -0,15 donc j= p.

la vitesse initiale est nulle :

x' (t=0)= -0,15*10sin (p) =0 est bien vérifiée

x (t) = 0,15 cos (10 t + p)

x' = -1,5 sin (10 t + p)

vitesse maximale : 1,5 m /s.

énergie mécanique = énergie potentielle élastique + énergie cinétique

E=0,5 k x² + 0,5 m v²

à t=0, pas d'énergie cinétique et x(t=0) = -0,15 m

E=0,5*10*(-0,15)² =0,225 J

la vitesse est maximale au passage à la position d'équilibre (toute l'énergie est sous forme cinétique) c'est à dire lorsque t = 0,25 période =0,25*0,628 =.0,157 s

0,225 =0,5*0,2v²maxi.

vitesse maxi = 1,5 m/s.


à suivre ...
retour - menu
à bientôt ...