| |
suspension d'un véhicule (France bac sept 2000)
|
||||||||
|
|
oscillations libres
|
La suspension d'un véhicule permet d’atténuer les vibrations verticales qui nuisent au confort et à la sécurité des passagers, par exemple lors du passage du véhicule dans un trou sur une route. Elle est constituée au niveau de chaque roue d’un ressort et d’un amortisseur (voir figure 1). On note G le centre d’inertie du véhicule. Lorsqu’on écarte le véhicule de sa position d’équilibre Go et qu’on le lâche, il oscille autour de cette position. L’amplitude des oscillations décroît suivant le degré d’amortissement de la suspension. L’ensemble du véhicule est équivalent à un oscillateur mécanique unique vertical amorti de masse m, de raideur k. On étudie le mouvement du centre d'inertie G seulement suivant la verticale. On repère son ordonnée y sur un axe Oy orienté vers le haut. La position du centre d'inertie du système à l’équilibre Go ( ressorts comprimés) est prise pour origine O de l'axe. 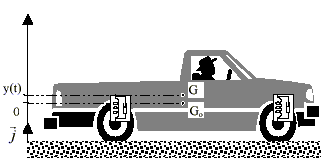 Données : •Masse : m = 1,5 × 10 3 kg. •Constante de raideur du ressort équivalent k = 6,0 × 10 5 N.m -1 . •La force de frottement qui s’exerce sur la masse m est
opposée à la vitesse du point G suivant la verticale, on peut l'écrire l est une constante positive appelée coefficient d'amortissement ou de frottement. On s'intéresse par la suite à l'influence de ce coefficient d'amortissement sur la qualité de la suspension. I. Oscillations libres de la suspension
|
|||||||
| |
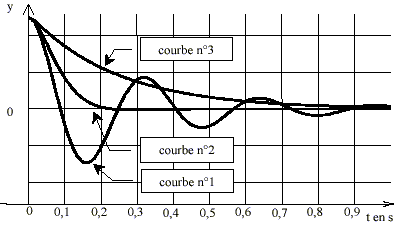
La courbe 3, la plus amortie (régime apériodique) correspond au cefficient d'amortissement le plus grand l3. pseudopériode lue sur le graphe (courbe 1) = 0,32 s. Le régime critique corespond à la courbe 2 avec l2= 5 × 10 4 kg.s -1
|
||||||||
|
oscillations forcées |
2. Test des amortisseurs, oscillations forcées Pour tester chacun des amortisseurs, on soumet les roues à une même excitation sinusoïdale produite par un support placé sous chaque roue . 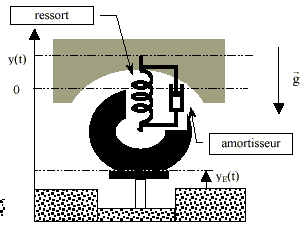 L’amplitude Ym des oscillations du centre d'inertie G du véhicule dépend alors de deux facteurs : l’amplitude YE et la fréquence fE de l’excitation sinusoïdale. La résolution des questions suivantes ne demande aucune mise en équation. On admettra que le comportement qualitatif du système s’apparente à celui d’un oscillateur amorti soumis à une force excitatrice sinusoïdale. L’amplitude YE de l’excitation sinusoïdale est maintenue constante. 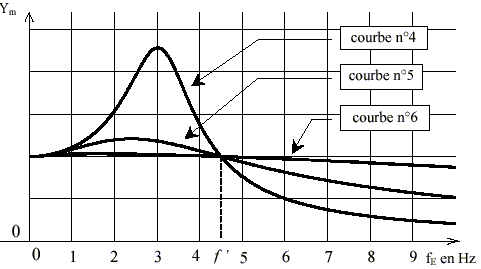 Le document ci dessus donne les courbes représentant Ym=g(fE) pour les trois valeurs du coefficient d’amortissement du paragraphe 1.
•pour des fréquences excitatrices fE > f ’ ? Quel amortisseur donne le meilleur compromis quelle que soit la fréquence excitatrice ? (Justifier chaque réponse)
|
||||||||
| |
courbe 4 : la fréquence à la résonance est égale à 3 Hz période propre de l'oscillateur = 2p racine carré (m/k) T= 2p rac carée(1500/6 105)=2p rac carrée (2,5 10-3)=0,314 s fréquence propre : 1/0,314 =3,18 Hz en accord avec la valeur trouvée sur le graphe. courbe 5 : la fréquence de résonance est proche de 2,5 Hz, donc la fréquence de résonance dépend du coefficient d'amortissement. pour les fréquences excitatrices fE telles que fE < f ’ , pour l'amortisseur correspondant à la courbe 6 (amortissement le plus grand soit l3) l'amplitude des oscillations est la plus faible. pour des fréquences excitatrices fE > f ’ , l'amortisseur correspondant à l1 (amortissement le plus faible) donne des oscillations de faibles amplitudes. l'amortisseur correspondant à l2 (amortissement moyen) donne un phénomène de résonance de faible amplitude et au delà de fE, les amplitudes des oscillations sont moins importantes qu'avec un oscillateur très amorti. Cet amortisseur donne le meilleur compromis.
|
||||||||
|
|
|