| |
oscillateur mécanique (groupe II bac juin 97)
|
||||||
|
|
étude graphique énergie frottements |
Dans un plan horizontal, on considère un système oscillant formé d'un mobile autoporteur lié à deux points fixes par l'intermédiaire de deux ressorts élastiques identiques, de masses négligeables, et de même axe. Le système, initialement au repos, est écarté de sa position d'équilibre en déplaçant le centre d'inertie G du mobile le long de l'axe des deux ressorts. L'ensemble des deux ressorts est équivalent à un ressort de constante de raideur k = 15,4 N.m-1. Une table à numériser permet la détermination des positions successives y de G dans un repère lié à la table ; la trajectoire de G est portée par l'axe y' y . Un logiciel de traitement de données permet d'afficher les points correspondant aux couples (t,y), (t,), ou toute autre fonction souhaitée, et d'en représenter les courbes.
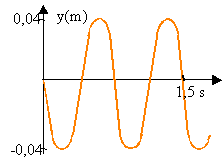
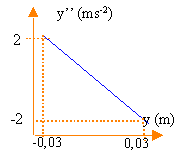
2. Les ressorts étant inchangés, un dispositif d'amortissement est désormais fixé sur le mobile. On réalise un nouvel enregistrement, représenté ci dessous.
En utilisant deux valeurs consécutives de la valeur maximale de y, donner un ordre de grandeur du pourcentage de l'énergie perdue par l'oscillateur au cours d'une période. Quelles sont les causes physiques de la dissipation ?
|
|||||
| |
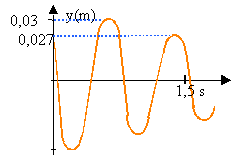
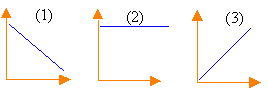
T=0,75 s. la pulsation w est égale à 2p / T=6,28 /0,75 = 8,37 rad s-1. l'amplitude Ym est égale à 0,04 m. l'équation différentielle peut s'écrire : y" = -w²y fonction linéaire décroissante de coefficient directeur -w². déterminer ce coefficient à partir du graphique : -4 /0,06 = -66,66 d'où w = 8,16 rad s-1. valeur théorique wo²= k/m =15,4 /0,22 =70 soit wo =8,36 rad s-1 en accord avec les valeurs précédentes l'énergie mécanique est la somme de l'énergie potentielle élastique et de l'énergie cinétique E = 0,5 ky² + 0,5 my'² E = 0,5 k ( y² + m/k y'²) avec wo²= k/m 2E / k = C = (y² +y'² / w0 ²) Lorsque y =Ym alors toute l'énergie est sous forme potentielle élastique. E = 0,5 kY²m l'énergie mécanique se conserve . E = 0,5 kY²m = 0,5k (y² +y'² / w0 ²) C = Y²m = 0,04² = 0,0016 m² E en fonction du temps, fonction constante : graphe (2) avec E en ordonnée C = (y² +y'² / w0 ²) s'écrit : y² = C- y'² / w0 ². fonction affine décroissante donc graphe (1) avec y² en ordonnée du fait des frottements mécaniques, l'oscillateur s'amorti; l'énergie mécanique diminue au cours du temps. Lorsque y =Ym, toute l'énergie est sous forme potentielle élastique, proportionnelle à Y²m. à la date t : E1= 0,5 k 0,03² = 0,5*15,4*0,03²= 6,93 mJ à la date t+T, E2 =0,5 k 0,027² =0,5*15,4*0,0027²= 5,61 mJ diminution d'énergie : 1,32 mJ soit environ 19% alors que l'amplitude ne diminuait que de 10%.
|
||||||
|
|
|