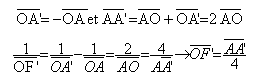| |
photocopieur ( France bac juin 99)
|
||||||
| |
|
||||||
|
|
reproduction grandeur nature du document |
Un photocopieur permet la reproduction d’un document original de surface S. Le système optique comporte entre autre un objectif constitué de plusieurs lentilles. L’image de l’ original est recueillie sur un tambour photosensible. Si g est le grandissement du système optique, la surface S’ de la photocopie est : S' = g²S. L’objectif du système optique est modélisé à l’aide du matériel d’optique d’un lycée. On place sur un banc optique :
L’axe optique principal est orienté dans le sens de propagation de la lumière. O est le centre optique de la lentille, A un point objet placé sur l’axe principal, A’ le point image de A et F’ le foyer principal image. L’objectif est assimilé à une lentille mince convergente L de centre optique O et de distance focale f '.
|
|||||
| |
Une lentille convergente donne d'un objet réel une image réelle renversée. grandissement g = -1
|
||||||
|
agrandissement d'un document |
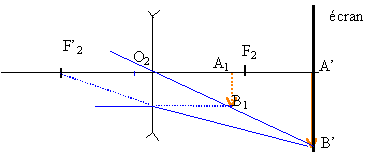
Dans ce cas l’objectif du système optique est modélisé en utilisant deux lentilles : une lentille convergente L1 de vergence C1=5,0 d ; une lentille divergente L2 de vergence C2= -3.0d . Le centre optique O1 de la lentille L1 est placée à 60,0 cm de A ; la lentille L1 donne de AB l’image A1B1. La lentille L2 est placée à droite de L1. Son centre optique O2 est tel que mesure algébrique de O1O2 =8,6 cm. L2 donne de A1B1 l’image définitive A’B’ sur l’écran.
corrigé |
||||||
| |
à partir de la formule de conjugaison on trouve mesure algébrique de O1A1=0,3 m grandissement g1 =0,3 / (-0,6 ) = -0,5
mesure algébrique de O2A1 = -0,086+0,3 =0,214 m mesure algébrique de O2A' =1,286-0,6-0,086 = 0,6 m grandissement g2 = 0,6 / 0,214 = 2,8 grandissement du système g = g1 g2 = -0,5*2,8 = -1,4 la surface de la photocopie est proportionnelle à g²soit à 1,4² voisin de 2
|
||||||
|
réduction d'un document |
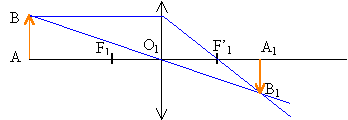
Dans ce cas, pour modéliser l’objectif, on permute les deux lentilles précédentes L1 et L2. La lentille L2 donne de AB l’image A2B2. La lentille L1 donne de A2B2 l’image définitive A’B’ sur l’écran.
corrigé |
||||||
| |
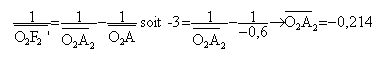
grandissement g1 =-0,214 / (-0,6 ) = 0,36 mesure algébrique de O2A1 = -0,086-0,214 = -0,3 m mesure algébrique de O2A' =1,286-0,6-0,086 = 0,6 m grandissement g2 = 0,6 / (-0,3 )= -2 grandissement du système g = g1 g2 = 0,36*(-2) = -0,72 la surface de la photocopie est proportionnelle à g²soit à 0,72² voisin de 0,51
|
||||||
|
|
|