| |
qualité d'une image ( bac septembre 2000)
|
||||||
| |
|
||||||
|
|
position et ouverture du diaphragme |
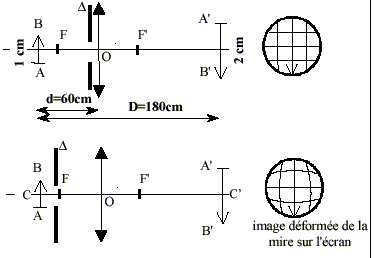
Le but de cet exercice est d'illustrer les difficultés à obtenir une image de bonne qualité. Pour cela, on dispose d’extraits d’un compte-rendu de travaux pratiques de deux élèves. Leurs formulations et leurs représentations ne sont pas toujours rigoureuses. On se propose de commenter leurs résultats et d’approfondir leurs conclusions. a) Expérience
corrigé |
|||||
| |
grandissement : mesure algébrique de l'image divisée par la mesure algébrique de l'objet. D'après les notations c'est aussi p' / p. d'après les dimensions de l'objet et de l'image le grandissement est -2 (le signe moins traduit une image inversée par rapport à l'objet) p= -0,6 m et p'= 1,2 m : on confirme la valeur -2 du grandissement. placer le diaphragme contre la lentille (position fixe) conditions de Gauss. choisir des diaphragmes de différentes ouvertures (diamètres différents) écran fixe déplacer l'objet afin de déterminer les positions extrèmes donnant une image nette sur l'écran. faire de même pour chaque diaphragme.
|
||||||
|
irisation de l'image |
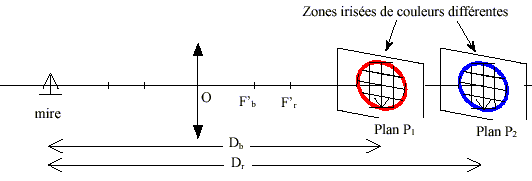
L’image d’un objet en lumière blanche peut être colorée sur son contour. Ceci est dû à la décomposition de la lumière : on dit que l’image est irisée. détermination des distances focales en lumière bleue et en lumière rouge : On a réalisé l’image de la mire sur le mur de la classe suffisamment éloigné de la lentille pour être considéré à l’infini. On a trouvé ainsi les distances focales f'b= 39,0 cm en lumière bleue et f'r= 40,5 cm en lumière rouge. On a placé la mire à d = 60,0 cm de la lentille. On a déterminé les positions où devraient se former les images en lumière bleue et en lumière rouge. On a trouvé en lumière bleue que l’image se forme dans un plan P1 situé à la distance Db = 161,4 cm et en lumière rouge dans un plan P2 à Dr = 184,6 cm (voir schéma ci-dessous). Observation en lumière blanche : En déplaçant l’écran, on a obtenu une image tantôt irisée en rouge, tantôt irisée en bleu comme montré sur le schéma ci-dessous.
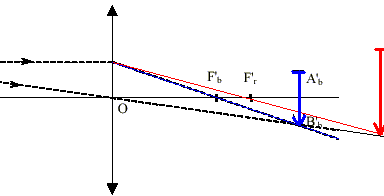
La figure n’est pas à l'échelle. Les foyers et images en lumière bleue sont repérés par la lettre b en indice et ceux en lumière rouge par la lettre r en indice. 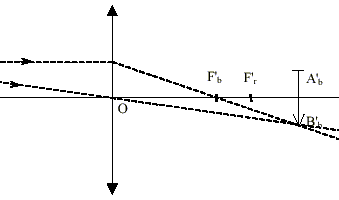
|
||||||
| |
Lorsque l'image se forme à l'infini, l'objet est au foyer principal objet. Il suffit alors de mesurer la distance lentille objet pour trouver la distance focale de la lentille.
|
||||||
|
|
|
||||||