| |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
histoire de pendules |
En 1671, Richer, un astronome français, part pour Cayenne en Guyanne, pour effectuer un pointé précis de la planète Mars et déterminer ainsi la distance Terre-Mars. Mais en réalisant ses expériences, Richer fait une découverte inattendue : en réglant ses horloges, il constate en effet que le même pendule bat plus lentement à Cayenne qu'à Paris. (d'après Newton et la mécanique céleste). Donnée : La période d'un pendule simple constitué d'une petite boule accrochée à un fil inextensible est T = 2p racine carrée( l / g).
corrigé |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
La grandeur physique expliquant cette différence doit intervenir au dénominateur dans l'expression de la période. De plus cette grandeur doit être plus faible à Cayenne ( proche de l'équateur) qu'à Paris. Cette grandeur est l'accélération de la pesanteur, notée g: elle vaut 9,8 N kg-1 à Paris et seulement 9,78 N kg-1 à l'équateur. La terre étant une sphère imparfaite, plus bombée à l'équateur et plus aplatie aux poles.
St Hélène et Cayenne sont proches de l'équateur. Paris et Londres sont à peu près à la même latitude. A St Hélene,le pendule bat plus lentement (voir explication ci dessus). T ² =4p² longueur / 9,8 d'où longueur = 9,8 T ² / (4p ²) L= 9,8 *1 /(4*3,14²) = 0,25 m. à la montagne g sera d'autant plus petit que l'altitude sera plus élevée. ( g diminue de 1% à une altitude de 30 km). Donc le pendule bat plus lentement à la montagne qu' à la mer. Celui qui est à la montagne rentrera plus tard, car son horloge retarde.
Le pendule le plus long a la plus longue période. La longueur de l'un étant 9 fois plus grande que la longueur de l'autre, la période de l'un sera 3 fois plus grande que celle de l'autre. Le pendule ( celui ci) ayant une longueur 9 fois plus petite effectue 3 oscillations pendant que celui là (longueur 9 fois plus grande) effectue une oscillation.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
mesurer l'intensité de la pesanteur |
On souhaite mesurer la valeur de l'intensité de la pesanteur
en utilisant un pendule simple. La relation donnant l'expression de la
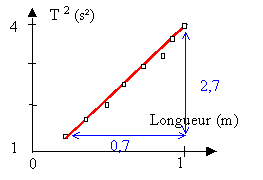
période T d'un pendule simple est : T2 = 4 p2 L / g. Les mesures conduisent aux résultats suivants :
corrigé |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
4 p² / g =3,9 d'où g = 4*3,14 ²/ 3,9 = 10,1 N / kg.
coefficient directeur de la droite : 2,7 / 0,7 =3,9 4 p² / g =3,9 d'où g = 4*3,14 ²/ 3,9 = 10,1 N / kg.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
satellites GPS |
La constellation GPS est un ensemble de satellites artificiels utilisés pour le positionnement à la surface de la terre. Ces satellites décrivent des orbites circulaires de rayon R=26400 km centrées sur le centre de la terre. Leur vitesse est constante, égale à 3,9 km / s.
corrigé |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
période = durée pour effectuer un tour . circonférence (km) = vitesse (km / s) fois période (s) période = T =165 792 / 3,9 = 42 510 s = 708min 31 s = 11h 48 min distance parcourue entre 2 "top" successifs : vitesse (km / s ) fois temps (s) = distance (km) 3,9 * 10-5 =3,9 10-5 km = 3,9 10-2 m = 3,9 cm
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
descente du poids d'une horloge |
Dans les horloges rudimentaires, une masse accrochée à un fil enroulé autour de l'axe d'une aiguille, faisait tourner l'aiguille en tombant. La chute était régulée par le balancier gràce au système d'échappement.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
durée de fonctionnement : 0,0628 m en une minute . 1,5 / 0,0628=23,88 min 0,0628 m en une heure 1,5 / 0,0628=23,88 heures
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
fréquence période |
corrigé |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
1 MHz = 106 Hz période = 1 / 6 108 = 1,666 10-9 s = 1,666 ns. 15 périodes correspondent à 12,3 s période = 12,3 / 15 = 0,82 s fréquence = 1/ 0,82 = 1,22 Hz
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|