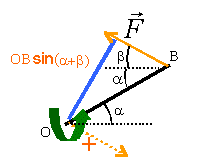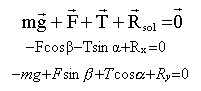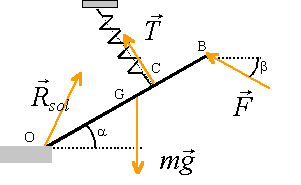
Aurélie dec 2000


devoirs 1ère S : couples de forces




Google



1

équilibre d'un pont

Masse OB tige homogène m=20 kg ;longueur : 1 m ; BC=20 cm a=20° b=30°

Ressort : raideur k L0=0,4 m L=50 cm ;Force F=50 N

On étudie OB à l'équilibre :

  1. Représenter les couples associés.
  2. Exprimer les moments en O de ces couples.
  3. Exptimer puis calculer la tension.En déduire la raideur.
  4. En écrivant que la somme des forces est nulle , exprimer puis calculer les caractéristiques de l'action du sol notée R.

corrigé


 

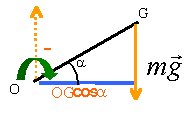
moment : -mgOGcosa.

-20*9.8*0,5*cos(20) = -92 Nm

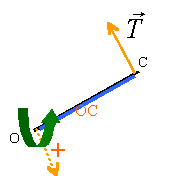
moment : T OC

T *0,8 Nm

moment : F OB sin(a+b).

50*1*sin50= 38,3 Nm.

l'action du sol n'a pas d'effet de rotation.

A l'équilibre la somme des moments est nulle :

F OB sin(a+b) +T OC-mgOGcosa=0

d'où T= [mgOGcosa- F OB sin(a+b)] /OC

38,3 +T *0,8-92 =0

T= 67,1 N

tension (N) = raideur (Nm-1) fois allongement (m)

allongement = différence de longueur du ressort = 0,1 m

raideur = 67,1 / 0,1 = 671 N m-1.

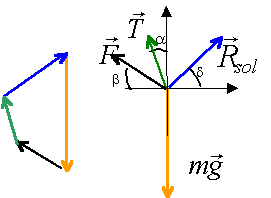
A l'équilibre la somme vectorielle des forces appliquées au pont OB est nulle.

Rx = 66,25 N

Ry = 113 N

d =tan-1 (113/66,25)= 59,6 °




à suivre ...
retour - menu
à bientôt ...