|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Les lampes halogènes basse tension sont de plus en plus utilisées pour des raisons de sécurité (tension admise même dans les pièces d'eau) mais aussi pour la lumière chaleureuse qu'elles procurent. Le dispositif étudié agrémente encore leur utilisation en produisant un allumage et une extension progressive ainsi qu'un réglage de l'intensité lumineuse en fonction de l'éclairage ambiant. Le synoptique présente globalement les fonctions intervenant dans ce système. 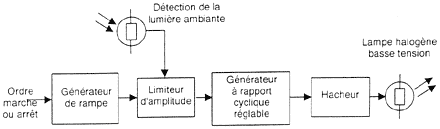
Indications : tous les composants sont considérés comme parfaits : - Notation des valeurs instantanées des grandeurs variables au cours du temps : v pour v(t), i pour i(t), ... - Les circuits intégrés ont une impédance d'entrée infinie et une impédance de sortie nulle - Les amplificateurs opérationnels ont leurs tensions de saturation confondues avec les tensions d'alimentation - Les tensions d'alimentation sont les suivantes : Pour les amplificateurs opérationnels :± VCC = ± 15 V; pour le circuit logique :VCC = 15 V ; pour le hacheur : VDD = 12 V. La lampe halogène LH soumise à une tension continue U, traversée par un courant d'intensité I, absorbe une puissance P et produit un flux lumineux . Le constructeur indique les caractéristiques nominales suivantes: U=12 V; P= 36 W; F= 3000 lm. Une étude expérimentale de la lampe alimentée sous tension variable a permis d'obtenir la courbe U(I) : 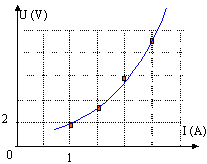 Par ailleurs, une mesure qualitative du flux lumineux montre que celui-ci croît avec la tension appliquée à la lampe.
corrigé |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
La caractéristique U(I) n'est pas une droite : la lampe n'est pas un dipôle linéaire. La résistance n'est pas constante, elle varie en fonction du courant appelé. Pour des valeurs de U données, les valeurs de I correspondantes sont déduites de la caractéristique U(I). On en déduit alors la puissance :
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
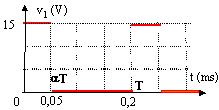
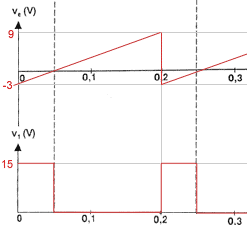
étage de puissance : la lampe est alimentée par un hacheur dont le schéma est donné : 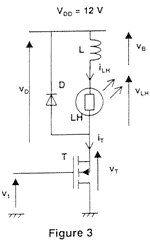 Le transistor T fonctionne en commutation et se comporte comme un interrupteur à savoir : - si v1 > 3 V, vT = 0 V (interrupteur fermé) ; - si v1 = 0 V, iT = 0 A (interrupteur ouvert). La bobine d'inductance L maintient le courant iLH toujours strictement positif. La diode D, supposée parfaite, se comporte comme un interrupteur ouvert ou fermé.
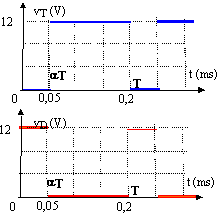
corrigé vD = vB + vLH <vD> = <vB> + <vLH> avec <vB> = 0 d'où <vD> = <vLH>
Lorsque v1 = 15 V, l'interrupteur est fermé, vT = 0 V et la diode est bloquée : vD = vDD - vT avec vT = 0 V Soit : vD = vDD = 12 V Lorsque v1 = 0 V, l'interrupteur est ouvert et la diode est passante, donc vD = 0 V (diode parfaite) D'où
vT = vDD - vD et
vT = vDD
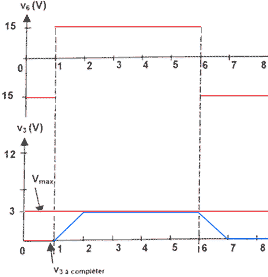
soit < vD > = a T *12 / T = 12 a a = 0,25 <vD> = a vDD = 0,25* 12 = 3 V D'après le graphique de la question 2) on a : flux lumineux = F3 car <vD> = u = 3 V
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
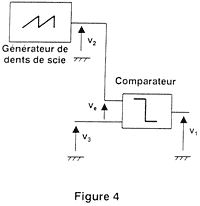
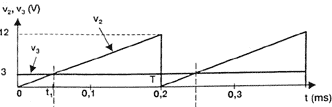
la commande du hacheur : La tension v1 de commande du hacheur est délivrée par le dispositif représenté :
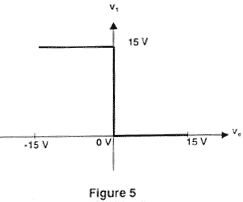
corrigé Lorsque l'entrée ve est négative, la sortie v1 est positive : le comparateur est inverseur. ve = v2 - v3
v2 = at + b D'après le graphe ci-dessus, b = 0 V ; a = 12/0,2 = 60 V/s v2(t1) = v3 donc v3 = at1 et t1 = v3/a a = t1/T = v3/aT = 3/(60* 0,2) = 0,25 Si v3 > 12 V, ve est négative sur toute la période et v1 = 15 V. Dans ce cas t1 = T donc a = 1. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
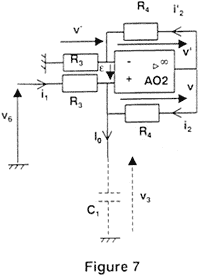
élaboration de la tension v3 : Le dispositif délivrant la tension v3 est représenté ci-dessous : 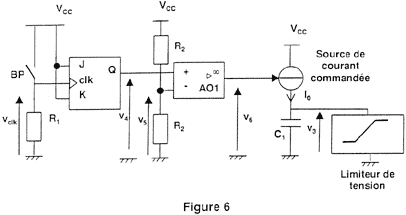
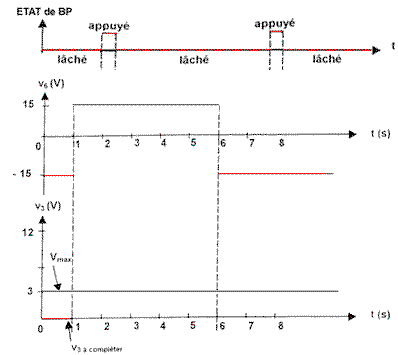
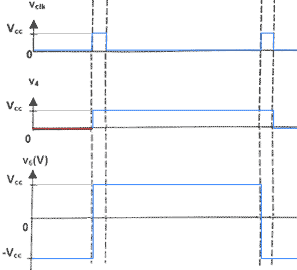
corrigé tension v4 : BP lâché : vclk = 0 V ; BP appuyé : vclk = vcc v4 est initialement nulle. Sur front montant de vclk, v4 = vcc. v4 est maintenant égale à vcc Sur front
montant de vclk, v4 = 0 car
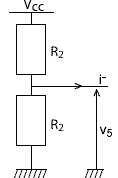
Qn = Etude de la tension v6 : a) AO1 fonctionne en saturation car il n'y a pas de rebouclage de la sortie sur l'entrée inverseuse. b) Le circuit AO1 est un comparteur simple. L'impédance d'entrée du circuit intégré est infinie donc i- = 0 On reconnait un diviseur de tension : v5 = R2 / (R2+R2 ) vcc = vcc/2 soit v5 = 7,5 V d) si v4 > v5 alors v6 = +vcc = 15 V si v4 < v5 alors v6 = -vcc = -15 V
Etude de la charge du condensateur : a) I0 = C dv3 /dt b) I0 = Kv6= C dv3 /dt d'où : dv3 /dt =Kv6/ C c) Kv6/ C = 50 10-6*15 / 250 10-6 = 3 V W-1 F-1. La tension v3 croît linéairement au cours du temps car sa dérivée est une constante. La représentation de v3(t) est une droite. Le terme Kv6/ C est le coefficient directeur de la droite. e)Kv6/ C = 50 10-6*(-15) / 250 10-6 = -3 V W-1 F-1. Etude de la source de courant commandée : a) I0 = i1 + i2 car i+ = 0 b) AO2 fonctionne en régime linéaire donc v+ = v- : i1 = (v6-v-) / R3. c) v' = v5 - v- ; v = v5 - v+ ; v- = v+ donc v' = v et i'2 = i2 d) i'2 = v- / R3 car i- = 0 e) I0 = i1 + i2 I0 =( v6-v-) / R3+ v- / R3= v6 / R3. f) R3 = 20 kW. g) v6 est la tension de sortie de AO1 qui a une impédance de sortie nulle.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
élaboration de la tension Vmax : le circuit qui délivre la tension Vmax est représenté ci-dessous 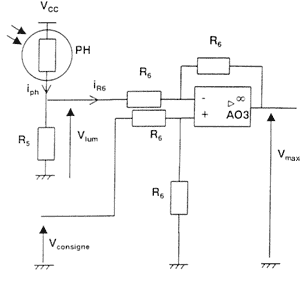 La tension
Vmax dépend de la consigne de
l'utilisateur d'une part et de l'intensité lumineuse
ambiante d'autre part. Une photorésistance PH sert de
capteur d'éclairement mesuré en lux. Sa
résistance RPH varie en fonction de
l'éclairement. Le constructeur indique les
caractéristiques suivantes :
corrigé Etude de la conversion éclairement-tension : Vlum= Rs/ (Rs + Rph) Vcc. Rs= Rph Vlum / (Vcc-Vlum) avec Rph= 400 W pour 1000 lux Rs= 1,6 kW. a) Vmax = Vconsigne - Vlum b) Vmax = 3V
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On se propose d'examiner la situation suivante : En plein jour (éclairement de 1000 lux), un utilisateur donne un ordre de mise en marche de la lampe par une action sur le bouton poussoir BP. La tension de consigne est préréglée à Vconsigne = 15 V.
corrigé Vmax commande le flux lumineux de la lampe et Vmax = Vconsigne - Vlum Lorsque le flux lumineux ambiant croît, Vlum croît, donc Vmax décroît et le flux lumineux de la lampe décroît. Lorsque le
flux lumineux ambiant décroît, Vlum
décroît, donc Vmax croît et le
flux lumineux de la lampe croît.
Tension
moyenne aux Tension
moyenne aux Lorsque le flux lumineux ambiant décroît, Vmax croît, donc le rapport cyclique augmente, ainsi que la valeur moyenne de la tension aux bornes de la lampe. Le flux lumineux de la lampe augmente
retour - menu |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||