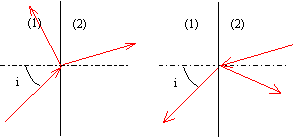|
|
||
|
||
|
exercice 1 : Une lame de verre d'indice ng est revêtue d'un film plastique d'indice nc : 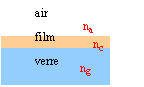
Exercice 2 : Soit une plaque de verre d'épaisseur Dx et d'indice de réfraction n placée entre une source S d'onde électromagnétique plane monochromatique de longueur d'onde l et un observateur O. 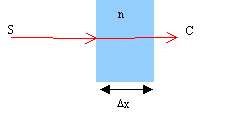
corrigé |
||
|
sous incidence normale pour le dioptre air -film R1 = [(nc/na-1) / (nc/na +1)]² sous incidence normale pour le dioptre film-verre R2 = [(ng/nc-1) / (ng/nc +1)]² écrire que R1 =R2 ; prendre la racine carrée ; faire les produits en croix et développer : (nc/na-1) / (nc/na +1) = (ng/nc-1) / (ng/nc +1) (nc/na-1)(ng/nc +1) = (ng/nc-1) (nc/na +1) 2 ng/nc = 2 nc/na on trouve la relation n²c = nang. angle d'incidence i =10° :
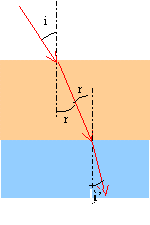
R1 = ½[sin(i-r) / sin(i+r) + tan(i-r) / tan( i+r)] dioptre air-film R2 = ½[sin(r-i') / sin(r+i') + tan(r-i') / tan( i'+r)] dioptre film-verre. premier dioptre : sin 10 = nc sin r second dioptre : nc sin r =1,52 sin i' d'où sin 10 = 1,52 sin i' et i' = 6,56°. n²c = nang permet de connaître nc puis l'angle r. nc = racine carrée (1,52) = 1,233 sin r = 0,142 et r = 8,16°. le calcul donne R1 = 0,100 et R2 = 0,1034 l'écart est de l'ordre de 3,5% principe de retour - menu inverse de la lumière : R= -R' R = ½[sin(i-r) / sin(i+r) + tan(i-r) / tan( i+r)] R' = ½[sin(r-i) / sin(i+r) + tan(r-i) / tan( i+r)] avec : sin(i-r) = - sin(r-i) et tan(i-r) = -tan(r-i) R= -R'. de plus R+T=1 si la surface n'absorbe pas la lumière T= 1-R T' = 1-R' = 1+R T T' = (1-R)(1+R) = 1-R². sans lame de vers la lumière traverse l'épaisseur Dx d'air en t seconde ( vitesse c) avec la lame de verre la lumière traverse la même épaisseur Dx en t1 seconde (vitesse v dans le matériau) Dx = c t et Dx = v t1 avec n = c/v t1-t = Dx ( 1/v - 1/ c) = Dx ( 1/c)[n-1]. or w (rad/s) = w = 2p fréquence = 2pc / l0 w(t1-t ) = 2p Dx/ l0 [n-1]. le déphasage d est proportionnel à 2p Dx / l0 (n-1).
expression du champ électrique : E0 exp(j(w t- d )) = E0 exp (jw t) exp( -j d ) d = 2p Dx / l0 (n-1). si d / l0 très inférieur à 1 : exp( -j d ) voisin de : 1-j d =1+ d exp (-jp/2) d'où : E0 exp (jw t) [1+ d exp (-jp/2)] E0 exp (jw t) +E0 d exp (-jp/2) . application numérique : d = 2p 10-3 / 10-3 (1,01-1)= 2p 10-2.
retour - menu |